सामग्री

• पाऊल टाकण्यासाठी
• पद्धत 3 पैकी 1: पहिले साधे कार्य
• पद्धत 3 पैकी: एका विशिष्ट निकालासाठी अपेक्षित मूल्याची गणना करत आहे
• पद्धत 3 पैकी 3: संकल्पना समजून घ्या
• टिपा
• गरजा

अपेक्षात्मक मूल्य एक सांख्यिकीय शब्द आहे आणि एखादी संकल्पना वापरली जाते की ती कार्यपद्धती कितपत उपयुक्त किंवा हानीकारक असेल हे ठरवते. अपेक्षित मूल्याची गणना करण्यासाठी, एखाद्या विशिष्ट परिस्थितीतील प्रत्येक परिणामाची आणि त्यासंबंधीची संभाव्यता किंवा विशिष्ट परिणाम उद्भवण्याची संभाव्यता याबद्दल चांगल्या प्रकारे समजून घेणे आवश्यक आहे. अपेक्षेच्या मूल्याची संकल्पना समजून घेण्यात मदत करण्यासाठी खाली दिलेल्या चरणांमध्ये काही उदाहरणांचे व्यायाम प्रदान केले जातात.

पाऊल टाकण्यासाठी

पद्धत 3 पैकी 1: पहिले साधे कार्य

1. विधान वाचा. आपण सर्व संभाव्य परिणाम आणि संभाव्यतेबद्दल विचार करण्यास प्रारंभ करण्यापूर्वी, आपण समस्या समजून घेणे महत्वाचे आहे. उदाहरणार्थ पासा खेळ ज्यासाठी प्रति गेम 10 डॉलर किंमत आहे. हेक्स डाय एकदा रोल केले जाते आणि आपले जिंकणे आपण रोल करीत त्या संख्येवर अवलंबून असते. जर 6 रोल केले तर आपण 30 डॉलर जिंकलात; एक 5 कमावते € 20; इतर कोणतीही संख्या काहीही मिळत नाही.
2. सर्व संभाव्य निकालांची यादी करा. हे दिलेल्या परिस्थितीत सर्व संभाव्य परिणामाची यादी करण्यास मदत करते. वरील उदाहरणात, 6 संभाव्य निकाल आहेत. हे आहेतः (1) रोल 1 आणि आपण $ 10 गमावले, (2) रोल 2 आणि आपण $ 10 गमावले, (3) रोल 3 गमावला आणि आपण $ 10 गमावले, (4) 4 रोल करा आणि आपण 10 डॉलर गमावले. , (5) एक 5 रोल करा आणि $ 10, (6) 6 6 रोल करा आणि 20 डॉलर जिंकून घ्या.
   • लक्षात ठेवा की प्रत्येक निकाल वर वर्णन केल्यापेक्षा 10 डॉलर्स कमी आहे, कारण आपल्याला कोणताही परिणाम न विचारता प्रथम प्रति खेळ 10 डॉलर द्यावे लागतील.
3. प्रत्येक निकालाची संभाव्यता निश्चित करा. या प्रकरणात, कोणत्याही 6 निकालांची संभाव्यता समान आहे. यादृच्छिक संख्येची रोलिंग होण्याची शक्यता 6 मध्ये 1 आहे. हे लिहिणे अधिक सुलभ करण्यासाठी आपण कॅल्क्युलेटरच्या सहाय्याने दशांश म्हणून अंश (1/6) लिहू: 0.167. ही संभाव्यता प्रत्येक निकालाच्या पुढे लिहा, विशेषत: जर आपल्याला प्रत्येक निकालासाठी भिन्न संभाव्यतेची समस्या सोडवायची असेल तर.
   • आपले 1/6 कॅल्क्युलेटर 0.166667 सारखे काहीतरी बनवू शकेल. अचूकतेचा बळी न देता गणना करणे सोपे करण्यासाठी आम्ही हे 0.167 पर्यंत गोल करतो.
   • आपल्याला अगदी अचूक निकाल हवा असल्यास तो दशांश बनवू नका, केवळ सूत्रात 1/6 प्रविष्ट करा आणि आपल्या कॅल्क्युलेटरवर गणना करा.
4. प्रत्येक निकालाचे मूल्य नोंदवा. संभाव्यतेनुसार परिणामाच्या परिणामी किती पैसे अपेक्षित मूल्यात योगदान देतात याची गणना करण्यासाठी परिणामाच्या Multi गुणाकार. उदाहरणार्थ, 1 रोलिंगचा परिणाम आहे - $ 10 आणि 1 रोलिंगची शक्यता 0.167 आहे. 1 टाकण्याचे मूल्य म्हणून (-10) * (0.167) आहे.
   • आपल्याकडे एकाच वेळी एकाधिक ऑपरेशन्स करू शकणारा कॅल्क्युलेटर असल्यास या परिणामांची गणना करण्याची आता गरज नाही. आपण संपूर्ण समीकरण प्रविष्ट केल्यास आपल्याला अधिक अचूक परिणाम मिळेल.
5. कार्यक्रमाचे अपेक्षित मूल्य मिळविण्यासाठी प्रत्येक निकालाचे मूल्य जोडा. वरील उदाहरणासह सुरू ठेवण्यासाठी, फासे खेळाचे अपेक्षित मूल्यः (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (10 * 0.167) + (20 * 0.167), किंवा - € 1.67. तर आपण या गेमवर (दर गेम) प्रत्येक वेळी 67 1.67 गमावण्याची अपेक्षा करू शकता.
6. अपेक्षित मूल्याची गणना केल्याचे परिणाम काय आहेत? वरील उदाहरणात, आम्ही निर्धारित केले की अपेक्षित नफा (तोटा) होईल - प्रति थ्रो. 1.67. 1 गेमसाठी हा एक अशक्य परिणाम आहे; आपण 10 डॉलर गमावू शकता, 10 डॉलर जिंकू शकता किंवा 20 डॉलर जिंकू शकता. परंतु दीर्घकाळात, अपेक्षित मूल्य एक उपयुक्त आणि सरासरी संभाव्यता असते. आपण हा गेम खेळत राहिल्यास, प्रति खेळ सरासरी अंदाजे 67 1.67 गमावाल. अपेक्षित मूल्याबद्दल विचार करण्याचा दुसरा मार्ग म्हणजे खेळासाठी काही खर्च (किंवा फायदे) नियुक्त करणे; आपल्याला फक्त हा गेम खेळायला पाहिजे जर आपल्याला तो फायदेशीर वाटला तर प्रत्येक वेळी त्यावर $ 1.67 खर्च करण्यासाठी पुरेसे आनंद घ्या.
   • जितक्या वेळा परिस्थितीची पुनरावृत्ती होते तितकेच अचूकतेने अपेक्षित मूल्य वास्तविक, सरासरी निकालाचे प्रतिनिधित्व करते. उदाहरणार्थ, कदाचित आपण सलग 5 वेळा गेम खेळत असाल आणि प्रत्येक वेळी आपण हरवाल, परिणामी सरासरी 10 डॉलर कमी होतील. तथापि, आपण हा खेळ आणखी 1000 वेळा खेळल्यास, सरासरी निकाल प्रति गेमच्या expected 1.67 च्या अपेक्षित मूल्याच्या जवळ आणि जवळ येईल. या तत्त्वाला "मोठ्या संख्येचा कायदा" म्हणतात.

पद्धत 3 पैकी: एका विशिष्ट निकालासाठी अपेक्षित मूल्याची गणना करत आहे

1. विशिष्ट नमुना येण्यापूर्वी आपल्याला पलटणे आवश्यक असलेल्या सरासरी नाण्यांची गणना करण्यासाठी या पद्धतीचा वापर करा. उदाहरणार्थ, आपण सलग दोनदा डोके न घेईपर्यंत पलटण्याकरिता अपेक्षित नाणी शोधण्यासाठी आपण या पद्धतीचा वापर करू शकता. अपेक्षेच्या मूल्यांबद्दल प्रमाणित समस्येपेक्षा ही समस्या जरा अवघड आहे, म्हणूनच आपण अपेक्षेच्या मूल्याच्या संकल्पनेशी परिचित नसल्यास प्रथम या लेखाचा वरील भाग वाचा.
2. समजा आपण x चे मूल्य शोधत आहोत. सलग दोन डोके मिळविण्यासाठी आपल्याकडे सरासरी फ्लिप करावी लागेल हे निश्चित करण्याचा प्रयत्न करीत आहात. उत्तर शोधण्यासाठी आम्ही आता एक तुलना करतो. आम्ही ज्या उत्तरांना शोधत आहोत त्याला आम्ही उत्तर देतो. आम्ही आवश्यक तुलना चरण-दर-चरण करतो. आमच्याकडे सध्या खालील गोष्टी आहेत:
   • x = ___
3. जर प्रथम फ्लिपने नाणे तयार केले तर काय होईल याचा विचार करा. अर्ध्या प्रकरणांमध्ये ही परिस्थिती असेल. जर अशी स्थिती असेल तर आपण एक रोल "वाया घालवला", तर सलग दोनदा डोके फिरवण्याची संधी बदलली नाही. नाणे टॉस प्रमाणेच, असे अपेक्षित आहे की सलग दोनदा डोके मिळण्यापूर्वी आपल्याला सरासरी वेळा टाकावी लागेल. दुस words्या शब्दांत, आपण बर्‍याचदा x x वेळा रोल कराल अशी अपेक्षा आहे, तसेच आपण आधीपासून खेळला आहे. समीकरण स्वरूपात:
   • x = (0.5) (x + 1) + ___
   • आम्ही इतर परिस्थितीबद्दल विचार करत राहिल्यामुळे आम्ही रिक्त जागा भरणार आहोत.
   • जर ते सोपे किंवा आवश्यक असेल तर आपण दशांशऐवजी अपूर्णांक वापरू शकता.
4. जेव्हा आपण आपले डोके फेकता तेव्हा काय होते याचा विचार करा. 0.5 (किंवा 1/2) शक्यता आहे की आपण प्रथम कप फेकून द्या. हे सलग दोनदा डोके फेकण्याच्या उद्दीष्ट्याजवळ जाताना दिसते, परंतु किती? दुसर्‍या रोलवरील आपल्या पर्यायांचा विचार करणे हे शोधण्याचा सर्वात सोपा मार्ग आहे:
   • जर दुसरा टॉस एक नाणे असेल तर आम्ही सुरवातीस परत आलो आहोत.
   • जर दुसरी वेळ देखील एक कप असेल तर आम्ही पूर्ण केले!
5. दोन घटना दोन्ही घडतील या संभाव्यतेची गणना कशी करावी हे जाणून घ्या. आम्हाला माहित आहे की आपल्याकडे 50% संधी आहे की आपण कप फेकून द्याल, परंतु आपण सलग दोनदा कप टाकण्याची संधी काय आहे? या संभाव्यतेची गणना करण्यासाठी, दोन्हीची संभाव्यता गुणाकार करा. या प्रकरणात ते 0.5 x 0.5 = 0.25 आहे. नक्कीच, हीच शक्यता आहे की आपण डोके फिरवाल आणि नंतर शेपटी कराल, कारण त्या दोघांनाही 0.5 होण्याची शक्यता आहे: 0.5 x 0.5 = 0.25.
6. "डोके, नंतर शेपटी" साठी परिणाम जोडा समीकरणात. आता आम्ही हा कार्यक्रम घडून येण्याची शक्यता मोजली आहे, तेव्हा आपण समीकरण विस्ताराकडे जाऊ शकतो. 0.25 (किंवा 1/4) शक्यता आहे की आम्ही पुढे न जाता दोनदा टाकणे वाया घालवू. परंतु, आम्हाला अद्याप निकाल मिळायला हवा आहे म्हणून आम्ही अजून सरासरीच्या एक्स नंबरची संख्या, तसेच आम्ही आधीच टाकली आहे. समीकरण स्वरूपात, हे (0.25) (x + 2) होते, जे आपण आता समीकरणात समाविष्ट करू:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + ___
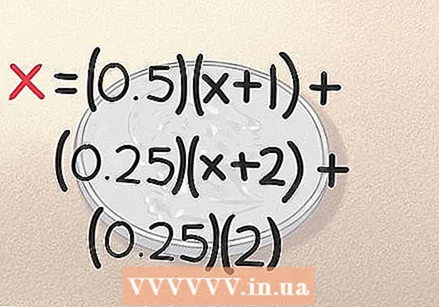7. समीकरणात "मथळा, शीर्षकासाठी" निकाल जोडा. जर आपण नाणी पहिल्या दोन टॉससह डोके टेकता, तर आपण पूर्ण केले. आपल्याला अगदी 2 थ्रो मध्ये निकाल लागला. जसे आपण आधी नमूद केले आहे की असे होण्याची शक्यता 0.25 आहे, म्हणून त्याचे समीकरण (0.25) (2) आहे. आमची तुलना आता पूर्ण झाली आहे:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + (0.25) (2)
   • आपण प्रत्येक संभाव्य परिस्थितीचा विचार केला आहे याची आपल्याला खात्री नसल्यास, समीकरण पूर्ण झाले आहे हे तपासण्याचा एक सोपा मार्ग आहे. समीकरणाच्या प्रत्येक भागाची पहिली संख्या घटना घडून येण्याची शक्यता दर्शवते. हे नेहमी 1 पर्यंत जोडेल. येथे, 0.5 + 0.25 + 0.25 = 1, म्हणून आम्हाला माहित आहे की आम्ही प्रत्येक परिस्थितीचा समावेश केला आहे.
8. समीकरण सुलभ करा. चला गुणाकार करून समीकरण थोडे सोपे करूया. लक्षात ठेवा, जर आपल्याला यासारखे कंसात काही दिसत असेल तर: (0.5) (x + 1), नंतर आपण कंसांच्या दुसर्‍या संचामध्ये असलेल्या प्रत्येक संज्ञेद्वारे 0.5 गुणाकार कराल. हे आपल्याला खालील देते: 0.5x + (0.5) (1), किंवा 0.5x + 0.5. समीकरणाच्या प्रत्येक टर्मसाठी हे करूया, नंतर या अटी एकत्रित करा जेणेकरून हे सर्व थोडे सोपे दिसते:
   • x = 0.5x + (0.5) (1) + 0.25x + (0.25) (2) + (0.25) (2)
   • x = 0.5x + 0.5 + 0.25x + 0.5 + 0.5
   • x = 0.75x + 1.5
9. X साठी सोडवा. कोणत्याही समीकरणाप्रमाणेच, समीकरणाच्या एका बाजूला x ची गणना करण्यासाठी आपल्याला वेगळे करणे आवश्यक आहे. लक्षात ठेवा, x चा अर्थ "सलग दोनदा डोके मिळविण्यासाठी आपल्याला नाणेफेक करण्याची आवश्यक सरासरी संख्या." जेव्हा आपण x ची गणना केली तर आपल्याला आपले उत्तरही सापडले.
   • x = 0.75x + 1.5
   • x - 0.75x = 0.75x + 1.5 - 0.75x
   • 0.25x = 1.5
   • (0.25x) / (0.25) = (1.5) / (0.25)
   • x = 6
   • सरासरी, दोनदा डोके टाकण्यापूर्वी आपल्याला 6 वेळा नाणे टाकावे लागेल.

पद्धत 3 पैकी 3: संकल्पना समजून घ्या

1. प्रत्यक्षात अपेक्षित मूल्य काय आहे. अपेक्षित मूल्य हे सर्वात स्पष्ट किंवा तार्किक परिणाम नाही. कधीकधी अपेक्षित मूल्य देखील दिलेल्या परिस्थितीत एक अशक्य मूल्य असू शकते. उदाहरणार्थ, 10 डॉलरपेक्षा जास्त नसलेल्या बक्षीस असलेल्या गेमसाठी अपेक्षेचे मूल्य + € 5 असू शकते. अपेक्षेचे मूल्य काय सूचित करते ते म्हणजे एखाद्या विशिष्ट घटनेचे किती मूल्य असते. एखाद्या खेळाचे अपेक्षित मूल्य + € 5 असल्यास आपण प्रत्येक गेमसाठी मिळणारा वेळ आणि पैसा वाचतो असे आपल्याला वाटत असल्यास आपण ते खेळू शकता. दुसर्‍या खेळाचे अपेक्षित मूल्य असल्यास - $ 20, नंतर आपण प्रत्येक गेमचे मूल्य 20 डॉलर्स असल्याचे आपल्याला वाटत असेल तरच आपण ते खेळा.
2. स्वतंत्र कार्यक्रमांची संकल्पना समजून घ्या. दैनंदिन जीवनात, आपल्यापैकी बर्‍याच जणांना असे वाटते की आपला भाग्य चांगला असतो जेव्हा काही चांगल्या गोष्टी घडतात आणि आपण उर्वरित दिवस त्या मार्गाने जाण्याची अपेक्षा करतो.तशाच प्रकारे, आपण असा विचार करू शकतो की आपल्याकडे अपघात झाला आहे आणि आता काहीतरी मनोरंजक गोष्ट घडली पाहिजे. गणितानुसार गोष्टी त्या मार्गाने जात नाहीत. आपण नियमित नाणे फेकल्यास, आपण डोके किंवा नाणे फेकून देण्याची तशीच शक्यता आहे. आपण यापूर्वी किती वेळा फेकले आहे याचा काही फरक पडत नाही; पुढील वेळी जेव्हा आपण ती टाकता तेव्हा तरीही त्याच मार्गाने कार्य करते. नाणे टॉस इतर टॉसपेक्षा "स्वतंत्र" आहे, त्याचा त्याचा परिणाम होत नाही.
   • नाणी टाकताना आपण भाग्यवान किंवा दुर्दैवी होऊ शकता असा विश्वास (किंवा इतर कोणत्याही संधीचा खेळ), किंवा आपली सर्व दुर्दैवीता आता संपली आहे आणि नशिब आपल्या बाजूला आहे हे देखील जुगार फसवणूक (किंवा जुगारीची लबाडी) असे म्हटले जाते. भाग्य आपल्या बाजूला आहे, किंवा त्यांना "भाग्यवान रेषा" वाटल्यास किंवा त्यांचे "नशिब आता वळणार आहे" असे वाटत असेल तेव्हा धोकादायक किंवा मूर्ख निर्णय घेण्याच्या लोकांच्या प्रवृत्तीशी याचा संबंध आहे.
3. मोठ्या संख्येने कायदा समजून घ्या. आपणास असे वाटेल की अपेक्षेचे मूल्य खरोखर उपयुक्त नाही, कारण एखाद्या परिस्थितीचा वास्तविक परिणाम काय आहे हे केवळ क्वचितच आपल्याला सांगते. जर आपण असे मोजले आहे की रूलेट गेमचे अपेक्षित मूल्य आहे - € 1, आणि आपण हा खेळ 3 वेळा खेळत असाल तर आपण सहसा समाप्त होऊ शकता - € 10, किंवा + € 60, किंवा काही इतर निकाल. अपेक्षेचे मूल्य आपल्या विचारापेक्षा अधिक उपयुक्त का आहे हे स्पष्ट करण्यासाठी "मोठा नंबर ऑफ लॉ" मदत करते: आपण जितके जास्त खेळता त्या सरासरी निकालाच्या अपेक्षेच्या मूल्याच्या जवळ जाईल. जेव्हा आपण मोठ्या संख्येने कार्यक्रम पाहता तेव्हा अंतिम निकाल अपेक्षित मूल्याच्या जवळ असणे चांगले असते.

टिपा

• अशा परिस्थितीत जिथे एकाधिक निकाल शक्य आहेत, आपण संगणकावर एक परिणाम आणि त्यांची संभाव्यता वापरून अपेक्षित मूल्याची गणना करण्यासाठी एक स्प्रेडशीट तयार करू शकता.
• वरील ulations गणने इतर चलनांमध्ये देखील कार्य करतात.

गरजा

• पेन्सिल
• कागद
• कॅल्क्युलेटर