सामग्री

• पाऊल टाकण्यासाठी
• पद्धत 1 पैकी 2: मूळ घटकांसह रूट पुलिंग
• 2 पैकी 2 पद्धत: कॅल्क्युलेटरशिवाय चौरस मुळे शोधणे
• लांब विभागणीसह
• प्रक्रिया समजून घ्या
• टिपा
• चेतावणी

कॅल्क्युलेटरच्या आगमनाच्या आधी, विद्यार्थी आणि प्राध्यापक दोघांनाही पेन आणि कागदासह चौरस मुळे मोजाव्या लागतात. या कधीकधी कठीण काम सोडविण्यासाठी विविध तंत्रे विकसित केली गेली होती, त्यातील काही अंदाजे अंदाज लावतात तर काही अचूक मूल्याची गणना करतात. काही सोप्या चरणांमध्ये संख्येचे स्क्वेअर रूट कसे शोधायचे हे जाणून घेण्यासाठी वाचा.

पाऊल टाकण्यासाठी

पद्धत 1 पैकी 2: मूळ घटकांसह रूट पुलिंग

1. आपली संख्या उर्जा घटकांमध्ये विभाजित करा. संख्येचे स्क्वेअर रूट शोधण्यासाठी ही पद्धत संख्येच्या घटकांचा वापर करते (संख्येनुसार ते अचूक उत्तर किंवा अंदाज असू शकते). द घटक दिलेल्या संख्येचा क्रमांकाचा क्रम असतो की त्या संख्येसह एकत्र गुणाकार केला जातो. उदाहरणार्थ, आपण असे म्हणू शकता की 8 चे घटक 2 आणि 4 च्या बरोबरीने आहेत कारण 2 × 4 = 8. दुसरीकडे परिपूर्ण वर्ग हे इतर पूर्णांकाचे उत्पादन आहेत. उदाहरणार्थ, २,,, 36 आणि perfect परिपूर्ण चौरस आहेत कारण ते अनुक्रमे,,, आणि to बरोबर आहेत द्वितीय उर्जा घटक, जसे तुम्हाला समजले असेल, ते देखील परिपूर्ण वर्ग आहेत. प्राइम घटकांचा वापर करून चौरस रूट शोधण्यासाठी प्रथम संख्येस त्याच्या दुसर्‍या शक्ती घटकांमध्ये विभाजित करण्याचा प्रयत्न करा.
   • खालील उदाहरण घ्या. आम्हाला 400 चे स्क्वेअर रूट सापडतील. सुरूवातीस, आम्ही संख्या पॉवर फॅक्टरमध्ये विभागली. 400 हे 100 चे गुणक असल्याने, आम्हाला माहित आहे की हे 25 द्वारे समान रीतीने विभाजित आहे - एक परिपूर्ण वर्ग. द्रुत रोटे आम्हाला सांगते की 400/25 = 16.16 एक परिपूर्ण स्क्वेअर देखील होते. तर 400 चे घन घटक आहेत 25 आणि 16 कारण 25 × 16 = 400.
   • आम्ही हे असे लिहितो: Sqrt (400) = Sqrt (25 × 16)
2. आपल्या दुसर्‍या उर्जा घटकांची चौरस मुळे घ्या. चौरस मुळांच्या उत्पादनाच्या नियमात नमूद केले आहे की कोणत्याही संख्येसाठी अ आणि बी, Sqrt (a × b) = Sqrt (a) × Sqrt (b). या मालमत्तेमुळे, आम्ही आता चौरस घटकांच्या चौरस मुळे घेऊ आणि उत्तर मिळविण्यासाठी एकत्र गुणाकार करू शकतो.
   • आमच्या उदाहरणात, आम्ही 25 आणि 16 च्या चौरस मुळे घेतो. खाली पहा:
     • चौरस (25 × 16)
     • चौरस (25) q चौरस (16)
     • 5 × 4 = 20
3. जर आपल्या क्रमांकाची अचूक गणना केली जाऊ शकत नसेल तर ती सरलीकृत करा. प्रत्यक्षात, आपण ज्या संख्येचे चौरस मुळ निश्चित करू इच्छित आहात ते 400 सारख्या छान चौरस असलेल्या छान गोलाकार संख्या असू शकत नाहीत. या प्रकरणांमध्ये, उत्तर म्हणून संपूर्ण संख्या मिळवणे शक्य होणार नाही. त्याऐवजी, आपण शोधू शकता अशा सर्व उर्जा घटकांचा वापर करून, आपण उत्तर एक लहान वापरण्यास सुलभ चौरस रूट म्हणून निर्धारित करू शकता. आपण हे पॉवर फॅक्टर आणि इतर घटकांच्या संयोजनात संख्या कमी करून आणि नंतर त्यास सुलभ करते.
   • आम्ही उदाहरण म्हणून 147 चा वर्गमूल घेतो. 147 दोन परिपूर्ण वर्गांचे उत्पादन नाही, म्हणून आम्हाला एक चांगले पूर्णांक मिळू शकत नाही. परंतु हे एका परिपूर्ण स्क्वेअर आणि दुसर्‍या क्रमांकाचे उत्पादन आहे - 49 आणि 3. आम्ही या माहितीचा उपयोग आपले उत्तर सर्वात सोप्या शब्दात लिहू शकतो:
     • चौरस (147)
     • = चौरस (49 × 3)
     • = चौरस (49) q चौरस (3)
     • = 7 q स्क्वेअर (3)
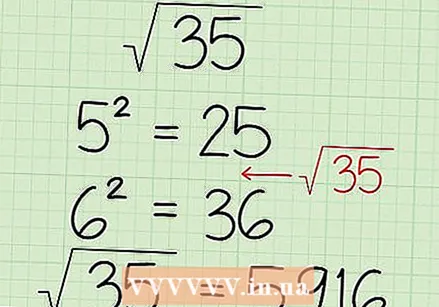4. आवश्यक असल्यास सरलीकृत करा. सर्वात सोप्या शब्दात चौरस रूट वापरुन, उर्वरित चौरस मुळांचा अंदाज घेऊन त्यांचे गुणाकार करुन उत्तराचा अंदाजे अंदाज घेणे साधारणपणे सोपे असते. आपला अंदाज सुधारण्याचा एक मार्ग म्हणजे आपल्या वर्गमूलमधील संख्येच्या दोन्ही बाजूंनी परिपूर्ण चौरस शोधणे. आपणास माहित आहे की आपल्या वर्गमूळातील संख्येचे दशांश मूल्य या दोन संख्येच्या दरम्यान कुठेतरी आहे, म्हणून आपला अंदाज देखील या संख्येच्या दरम्यान असावा.
   • चला आपल्या उदाहरणाकडे परत जाऊ. २ = and आणि १ = १ असल्याने, आपल्याला माहिती आहे की एसक़र्ट ()) हे १ ते २ दरम्यान आहे - बहुधा १ पेक्षा २ च्या जवळ आहे. आमचा अंदाज आहे की १.7. 7 × 1.7 = 11,9. जर आपण हे कॅल्क्युलेटरद्वारे तपासले तर आम्ही आपल्या उत्तराच्या अगदी जवळ आहोत हे पाहतो: 12,13.
     • हे मोठ्या संख्येसाठी देखील कार्य करते. उदाहरणार्थ, चौरस (35) अंदाजे 5 ते 6 (कदाचित 6 च्या जवळ) दरम्यान आहे. 5 = 25 आणि 6 = 36.35 25 आणि 36 दरम्यान आहे, म्हणून चौरस मूळ 5 ते 6 दरम्यान असेल. 35 हे अगदी 36 च्या खाली आहे म्हणून आम्ही काही प्रमाणात आत्मविश्वासाने सांगू शकतो की त्याचा वर्गमूल फक्त 6 पेक्षा कमी आहे. कॅल्क्युलेटरद्वारे तपासणी केल्याने आम्हाला सुमारे 5.92 चे उत्तर मिळते - आम्ही बरोबर होतो.
5. वैकल्पिकरित्या, पहिली पायरी म्हणून, आपण संख्या सुलभ करू शकता किमान सामान्य अनेक. जर आपल्याला सहजतेने संख्येचे मुख्य घटक (एकाच वेळी प्राइम नंबर देखील असतात असे घटक) सहज सापडले तर पॉवर फॅक्टर शोधणे आवश्यक नाही. कमीतकमी सामान्य गुणाकारांच्या संख्येवर संख्या लिहा. मग मूळ संख्येच्या जोड्या जुळण्यासाठी आपल्या घटकांमध्ये शोधा. जेव्हा आपल्याला जुळणारे दोन मुख्य घटक सापडतील तेव्हा त्यांना स्क्वेअर रूट आणि ठिकाणातून काढा अ या संख्येपैकी स्क्वेअर रूट चिन्हा बाहेर.
   • उदाहरणार्थ, आम्ही ही पद्धत वापरुन 45 चा वर्गमूल निर्धारित करतो. आम्हाला माहित आहे की = 45 = × × and आणि ते = = × ×. तर आपण असे स्क्वेअर रूट लिहू शकतो: स्क्वेअर (3 × × ×)). सरलीकृत चौरस रूट मिळविण्यासाठी फक्त 3 हटवा आणि चौरस रूटच्या बाहेर एक 3 ठेवा: ()) चौरस ()) आता आपण सहजपणे अंदाज लावू शकता.
   • अंतिम उदाहरण; आम्ही 88 चे वर्गमूळ निश्चित करतो:
     • चौरस (88)
     • = चौरस (2 × 44)
     • = वर्गमीटर (2 × 4 × 11)
     • = चौरस (2 × 2 × 2 × 11) आमच्या वर्गमूलमध्ये आमच्याकडे अनेक 2 आहेत. 2 प्रमुख असल्याने, आम्ही एक जोडी काढू आणि 2 मुळाच्या बाहेर ठेवू.
     • = सर्वात सोप्या शब्दांमध्ये आमचा स्क्वेअर रूट (2) स्क्वेअर (2 × 11) किंवा आहे (2) स्क्वेअर (2) चौरस (11) आता आपण Sqrt (2) आणि Sqrt (11) कडे जाऊ शकतो आणि आम्हाला हवे असल्यास अंदाजे उत्तर शोधू शकतो.

2 पैकी 2 पद्धत: कॅल्क्युलेटरशिवाय चौरस मुळे शोधणे

लांब विभागणीसह

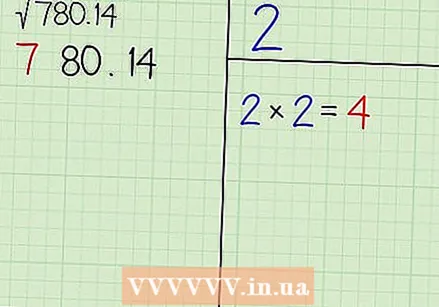
1. आपल्या संख्येचे अंक जोडीमध्ये विभाजित करा. ही पद्धत लांब प्रभाग सारखीच आहे, जी आपल्याला विभाजित करण्याची परवानगी देते अचूक अंकांप्रमाणे अंकांचे वर्गमूल. आवश्यक नसले तरी, कार्य करण्यायोग्य तुकड्यांमध्ये संख्या खंडित करणे निराकरण करणे सुलभ करते, विशेषत: जर ते लांब असेल. प्रथम कार्य क्षेत्रास 2 क्षेत्रामध्ये विभाजित करणारी अनुलंब रेषा काढा आणि नंतर उजव्या भागाच्या शिखरावर एक छोटी ओळ बनवा, त्यास खाली वरच्या भागामध्ये आणि खाली एका मोठ्या भागामध्ये विभाजित करा. नंतर दशांश बिंदूपासून प्रारंभ करुन संख्यांना जोड्या जोडा. या नियमांतर्गत, 79520789182.47897 "7 95 20 78 91 82.47 89 70" होते. वरच्या डाव्या भागात हा नंबर लिहा.
   • उदाहरणार्थ, 780.14 च्या वर्गमूलची गणना करू. आपल्या कार्याची जागा वरील प्रमाणे विभाजित करा आणि वरच्या डाव्या कोपर्‍यात "7 80, 14" लिहा. दोन ऐवजी आतापर्यंत डावीकडे फक्त एकच संख्या असल्यास ते ठीक आहे. त्यानंतर आपण योग्य क्षेत्राच्या शीर्षस्थानी उत्तर (780.14 चा वर्ग मूळ) लिहा.
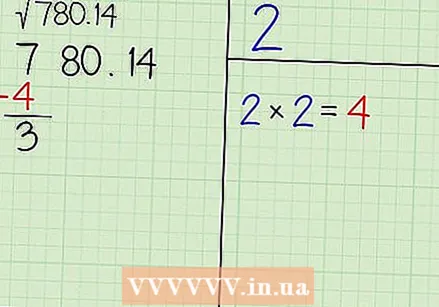
2. सर्वात मोठा पूर्णांक शोधा एन ज्याचा चौरस डावीकडील अंक किंवा संख्येपेक्षा कमी किंवा समान आहे. या संख्येपेक्षा कमी किंवा समान असा सर्वात मोठा वर्ग शोधा आणि नंतर या चौकाचा वर्गमूल शोधा. ही संख्या आहे एन. वरच्या उजव्या भागात ते लिहा आणि त्या भागाच्या खाली चतुष्पादात n चा वर्ग लिहा.
   • आमच्या उदाहरणात, डावीकडील सर्वात जास्त संख्या ही संख्या 7 आहे. कारण आपल्याला हे माहित आहे की 2 = 4 ≤ 7 3 = 9, आम्ही असे म्हणू शकतो एन = 2 कारण हा सर्वात मोठा पूर्णांक आहे ज्याचा वर्ग 7 पेक्षा कमी किंवा समान आहे. वरच्या उजव्या चौकोनावर 2 लिहा. हा उत्तराचा पहिला अंक आहे. खालच्या उजव्या चौकोनावर 4 (2 चा वर्ग) लिहा. पुढील चरणात ही संख्या महत्त्वपूर्ण आहे.
3. आपण मोजलेली संख्या वजा करा सर्वात डावीकडील अंक किंवा संख्येचा लांब विभाजनाप्रमाणे, पुढील चरण म्हणजे आपण मोजण्यासाठी नुकत्याच वापरलेल्या संख्येमधून वर्ग कमी करणे. डाव्या क्रमांकाखाली हा क्रमांक लिहा आणि त्यांना वजा करा. खाली उत्तर लिहा.
   • आमच्या उदाहरणात, आम्ही 4 अंतर्गत 7 लिहून त्यास वजा करू. हे देते 3 प्रतिसादात.
4. पुढील नंबर खाली हलवा. मागील संपादनात आपल्याला सापडलेल्या मूल्याच्या पुढे हे ठेवा. शीर्षस्थानी उजवीकडची संख्या दोन ने गुणाकार करा आणि तळाशी उजवीकडे लिहा. पुढील चरणात आपण करत असलेल्या बेरीजसाठी आपण नुकत्याच लिहलेल्या क्रमांकाच्या खाली जागा सोडा. येथे "_ × _ =" "लिहा.
   • आमच्या उदाहरणात, पुढील संख्या "80" आहे. डाव्या चतुर्भुज मध्ये 3 च्या पुढे "80" लिहा. नंतर वरच्या उजव्या क्रमांकाची संख्या २ ने गुणाकार करा. ही संख्या २ आहे, म्हणून २ × २ = 4.. तळाशी उजवीकडे "" "" लिहा, त्यानंतर पाठोपाठ _×_=.
5. उजवीकडे संख्या प्रविष्ट करा. बेरीजच्या रिक्त जागेत (उजवीकडे) सर्वात मोठा पूर्णांक प्रविष्ट करा जो गुणाकाराच्या परिणामाचा परिणाम डावीकडील सद्य संख्येपेक्षा कमी किंवा समान करेल.
   • आमच्या उदाहरणात, आम्ही 8 प्रविष्ट करतो आणि हे 4 (8) × 8 = 48 × 8 = 384 देते. हे 380 पेक्षा मोठे आहे. तर 8 खूप मोठे आहे, परंतु 7 कदाचित नाही. 7 भरा आणि निराकरण करा: 4 (7) × 7 = 329. 7 चांगले आहे कारण 329 380 पेक्षा कमी आहे. शीर्षस्थानी उजवीकडे 7 लिहा. 780.14 च्या चौरस मूळातील हा दुसरा अंक आहे.
6. डावीकडच्या सद्य क्रमांकावरून आपण नुकतीच गणना केलेली संख्या वजा. तर आपण सध्याच्या उत्तरापासून उजवीकडे गुणाकाराचा निकाल डावीकडे वजा करा. आपले उत्तर खाली थेट लिहा.
   • आमच्या उदाहरणात, आम्ही 380 वरून 329 वजा करतो आणि ते देते 51 परिणामी
7. चरण 4 पुन्हा करा. पुढील जोड्यांची संख्या 780.14 वरून हलवा. जेव्हा आपण स्वल्पविरामाने पोहोचता तेव्हा उजवीकडे उत्तरात स्वल्पविरामाने लिहा. नंतर वरच्या उजव्या क्रमांकाची 2 ने गुणाकार करा आणि वरील उत्तर ("_ × _") पुढे लिहा.
   • आमच्या उत्तरात आम्ही आता स्वल्पविराम लिहितो कारण आपल्याकडे हे 780.14 मध्ये देखील आढळते. पुढची जोडी (14) डावी चौकोनी खाली हलवा. २ x x २ =, 54, म्हणून आम्ही खालच्या उजव्या चौकोनावर "54 _ × _ =" लिहितो.
8. 5 आणि 6 चरण पुन्हा करा. सर्वात मोठी संख्या शोधा जी उत्तर देईल जी डावीकडील सद्य संख्येपेक्षा कमी किंवा समान आहे. निराकरण करा.
   • आमच्या उदाहरणात, 549 × 9 = 4941, जे डावीकडील संख्येपेक्षा कमी किंवा समान आहे (5114). 549. 10 = 5490, जे खूप जास्त आहे, त्यामुळे 9 आपले उत्तर आहे. पुढील शीर्ष उजवीकडील संख्या म्हणून 9 लिहा आणि डाव्या क्रमांकापासून गुणाकाराचा परिणाम वजा करा: 5114 -4941 = 173.
9. निकाल अचूक करण्यासाठी आपल्यास आवश्यक असलेल्या दशांश जागेच्या (शंभरावा, हजारव्या) संख्येसह उत्तर सापडल्याशिवाय मागील प्रक्रिया पुन्हा करा.

प्रक्रिया समजून घ्या

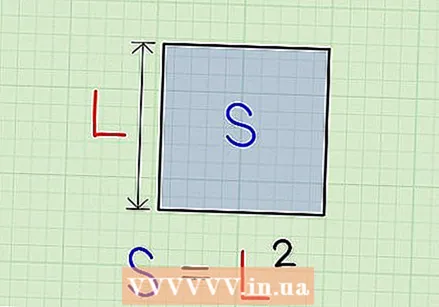1. आपण ज्याच्या चौरस रूटची गणना करू इच्छिता अशा संख्येचा विचार करा ज्याचे वर्ग चौरस हे एस. एखाद्या चौरसाचे क्षेत्रफळ एल आहे, जेथे एल त्याच्या एका बाजूची लांबी आहे, म्हणून आपल्या संख्येचे चौरस मूळ शोधून आपण त्या चौकोनाच्या बाजूच्या लांबीची गणना करण्याचा प्रयत्न करा.
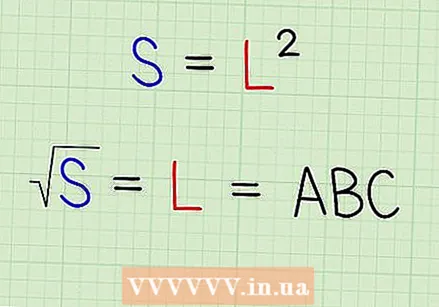2. आपल्या उत्तराचा प्रत्येक अंक पत्र द्या. एलचा पहिला अंक म्हणून व्हेरिएबल ए एंटर करा (आम्ही मोजू पाहत आहोत त्याचा वर्गमूल) बी हा दुसरा अंक, सी तिसरा आणि इतका
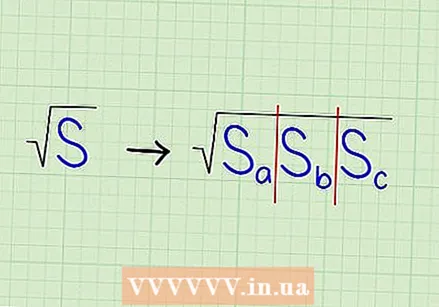3. आपण प्रारंभ करत असलेल्या नंबरच्या प्रत्येक "जोड्यांच्या संख्येला" एक पत्र द्या. व्हेरिएबल एस द्या_अ एस मधील आरंभिक पहिल्या जोडीला (आरंभिक मूल्य) एस._बी अंकांच्या दुसर्‍या जोडीला इ.
4. ही पद्धत आणि दीर्घ विभागातील संबंध समजून घ्या. चौरस रूट शोधण्याची ही पद्धत मूलत: एक लांब विभागणी आहे, जिथे आपण प्रारंभिक मूल्य त्याच्या चौरस रूटने विभाजित करा आणि उत्तर म्हणून वर्गमूल "द्या". लांब विभागणी प्रमाणेच, जिथे आपल्याला एका वेळी फक्त पुढील अंकात स्वारस्य असेल, आपणास एकाच वेळी फक्त पुढील दोन अंकांमध्ये स्वारस्य असेल (जे चौरस मुळाच्या पुढील अंकांशी संबंधित असेल).
5. सर्वात मोठा संख्या शोधा ज्यांचा वर्ग एस पेक्षा कमी किंवा समान आहे._अ आहे. आमच्या उत्तरातील पहिला अंक अ नंतर सर्वात मोठा पूर्णांक आहे ज्यांचा वर्ग एसपेक्षा जास्त नाही._अ (एए ≤ सा (ए + 1).) आमच्या उदाहरणात, एस_अ = 7, आणि 2² ≤ 7 3², म्हणून अ = 2.
   • लक्षात ठेवा की आपण लांब डिव्हिजन वापरुन 88962 चे विभाजन 7 केले तर प्रथम चरण समान आहे: आपण प्रथम 88962 (8) च्या पहिल्या अंकासह व्यवहार कराल आणि आपल्याला सर्वात मोठा अंक 7 ने गुणले पाहिजे जे 8 पेक्षा कमी किंवा समान असेल. निश्चित करा डी जसे की 7 × d ≤ 8 7 × (d + 1). या प्रकरणात, डी 1 च्या बरोबरीचे आहे.
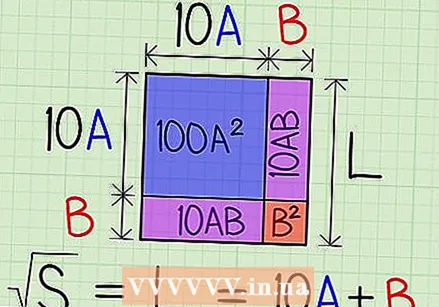6. आपण ज्या क्षेत्राचा शोध घेऊ इच्छित आहात त्या क्षेत्राची कल्पना करा. आपले उत्तर, आरंभिक मूल्याचे चौरस मूळ, एल आहे, जे क्षेत्र एस (प्रारंभिक मूल्य) असलेल्या चौकोनाच्या लांबीचे वर्णन करते. ए, बी आणि सी चे मूल्य एल मधील मूल्यांचे अंक दर्शवितात. हे सांगण्याची आणखी एक पद्धत म्हणजे 2-अंकी उत्तर, 10 ए + बी = एल आणि 3-अंकी उत्तरासाठी 100 ए + 10 बी + सी = एल इत्यादी.
   • आमच्या उदाहरणात (10 ए + बी) ² = एल = एस = 100 ए² + 2 × 10 ए × बी + बी². लक्षात ठेवा की 10 ए + बी आमचे उत्तर एल सह युनिट्सच्या स्थितीत बी आणि दशांश स्थितीत ए चे प्रतिनिधित्व करते. उदाहरणार्थ, जर ए = 1 आणि बी = 2, तर 10 ए + बी ही संख्या 12 आहे. (10 ए + बी) ² संपूर्ण चौकाचे क्षेत्र आहे, तर 100A² सर्वात मोठे आतील चौरस क्षेत्र आहे, बी सर्वात लहान चौरस क्षेत्र आहे 10 ए × बी उर्वरित प्रत्येक आयताचे क्षेत्र आहे. या लांब, गुंतागुंतीच्या प्रक्रियेद्वारे आम्ही चौकाचे क्षेत्र आणि आयताकृतींचा भाग जोडून संपूर्ण चौकाचे क्षेत्र शोधू शकतो.
7. एस वजाबाकी ए._अ. संख्या जोडा. (एस._बी) एस एस पासून खाली एस._अ एस._बी स्क्वेअरचे जवळजवळ एकूण क्षेत्र आहे, जिथून तुम्ही सर्वात मोठे आतील चौरस क्षेत्र नुकतेच वजा केले. उरलेले संख्या एन 1 आहे, जे आम्ही चरण 4 मध्ये प्राप्त केले (आमच्या उदाहरणात एन 1 = 380). एन 1 2 × 10 ए × बी + बी als (2 आयतांचे क्षेत्रफळ तसेच लहान चौरसाचे क्षेत्रफळ) इतके आहे.
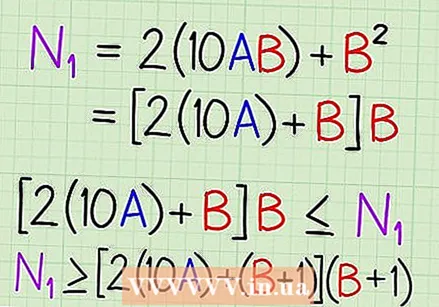8. एन 1 = 2 × 10 ए × बी + बी² पहा, एन 1 = (2 × 10 ए + बी) × बी म्हणून देखील लिहिलेले आमच्या उदाहरणात, आपल्याला आधीपासूनच एन 1 (380) आणि ए (2) माहित आहे, म्हणून आता आपल्याला बी शोधणे आवश्यक आहे. बी कदाचित पूर्णांक नाही, म्हणून आपल्याकडे असणे आवश्यक आहे प्रत्यक्षात सर्वात मोठा पूर्णांक बी शोधा, जसे की (2 × 10 ए + बी) × बी ≤ एन 1. तर आता आपल्याकडे: एन 1 (2 × 10 ए + (बी + 1)) × (बी + 1).)
9. समीकरण सोडवा. हे समीकरण सोडविण्यासाठी, A ला 2 ने गुणाकार करा, त्यास दहा वर हलवा (10 ने गुणाकार करा), बीला युनिटमध्ये टाका आणि निकाल बीने गुणाकार करा. दुस words्या शब्दांत, (2 × 10A + B) × बी. आपण चरण 4 च्या खालच्या उज्वल चौकोनावर "एन_ × _ =" (एन = 2 with ए सह) लिहिता तेव्हा आपण काय करता हे निश्चित करता चरण 5 मध्ये आपण रेषाच्या खाली बसणार्‍या सर्वात मोठा पूर्णांक बी निश्चित करता, तर (2 × 10A + बी) × बी ≤ एन 1.
10. एकूण क्षेत्रापासून क्षेत्र (2 × 10 ए + बी) × बी वजा करा. हे क्षेत्र एस- (10 ए + बी) देते ² जे आपण अद्याप खात्यात घेतलेले नाही (आणि आपण खालील नंबरची गणना करण्यासाठी त्याच प्रकारे वापरता).
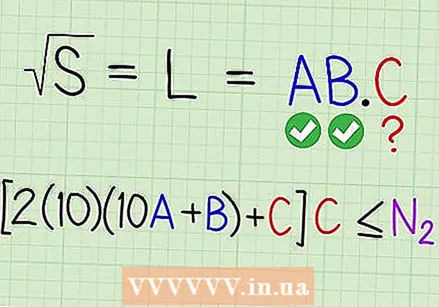11. पुढील अंकांची गणना करण्यासाठी, प्रक्रिया पुन्हा करा. क्रमांकाची पुढील जोडी एस वरुन खाली हलवा (एस_सी) डावीकडून एन 2 मिळविण्यासाठी आणि आता आपल्याकडे असलेला सर्वात मोठा सी शोधण्यासाठी: (2 × 10 × (10 ए + बी) + सी) × सी ≤ एन 2 ("एबी" नंतरच्या दोन-अंकी क्रमांकाच्या समान) "_ × _ =" द्वारा आपण येथे प्रविष्ट करू शकता अशी सर्वात मोठी संख्या निश्चित करा, जे आपल्याला उत्तर देईल जे एन 2 पेक्षा कमी किंवा त्या समान असेल.

टिपा

• स्वल्पविरामाने दोन ठिकाणी हलविणे (100 चे घटक) संबंधित चौरस मुळामध्ये स्वल्पविराम एका स्थानाद्वारे हलविते (10 एक घटक).
• उदाहरणार्थ, 1.73 ला "उर्वरित" मानले जाऊ शकते: 780.14 = 27.9² + 1.73.
• ही पद्धत केवळ दशांश (दशांश) प्रणाली नव्हे तर कोणत्याही संख्या प्रणालीसाठी कार्य करते.
• आपल्याला पाहिजे असलेली गणिते मोकळ्या मनाने मोकळ्या करा. काही लोक ज्याच्या वर्गमूलची गणना करू इच्छित आहेत त्या संख्येच्या वर ते लिहितो.
• वैकल्पिक पद्धत खालीलप्रमाणे आहेः √z = √ (x ^ 2 + y) = x + y / (2x + y / (2x + y / (2x + ...))). उदाहरणार्थ, 780.14 च्या वर्गमूलची गणना करण्यासाठी, पूर्णांक घ्या ज्यांचा वर्ग 780.14 (28) च्या सर्वात जवळ आहे, म्हणून = 780.14, x = 28 आणि y = -3.86. भरणे आणि अंदाज लावल्यास आम्हाला x + y / (2x) मिळेल आणि हे (सरलीकृत अटी) 78207/2800 किंवा सुमारे 27.931 (1) देते; खालील टर्म, 4374188/156607 किंवा सुमारे 27.930986 (5). प्रत्येक टर्म मागील एकापेक्षा जवळजवळ 3 दशांश अचूक स्थान जोडते.

चेतावणी

• दशांश बिंदूपासून जोड्यांमध्ये संख्या निश्चित करण्याचे सुनिश्चित करा. "79 52 07 89 18 म्हणून 79520789182.47897 चे विभाजन करीत आहे 2,4 78 97 "चुकीचा निकाल देते.