सामग्री

• पाऊल टाकण्यासाठी
• 4 पैकी भाग 1: मॅट्रिक्स रेखांकन
• 4 पैकी भाग 2: मॅट्रिक्सद्वारे सिस्टम सोडविण्याकरिता ऑपरेशन्स शिकणे
• 4 पैकी भाग 3: आकाशगंगाचे निराकरण करण्यासाठी चरण विलीन करा
• 4 चे भाग 4: आपले समाधान शोधत आहे
• टिपा

मॅट्रिक्स हा ब्लॉक स्वरूपनात संख्या दर्शविण्याचा एक अतिशय उपयुक्त मार्ग आहे, जो आपण नंतर रेषीय समीकरणांच्या सिस्टमचे निराकरण करण्यासाठी वापरू शकता. आपल्याकडे फक्त दोन व्हेरिएबल्स असल्यास आपण कदाचित वेगळी पद्धत वापरु शकता. या इतर पद्धतींच्या उदाहरणांसाठी समीकरणांची एक यंत्रणा सोडवण्याबद्दल याबद्दल वाचा. परंतु आपल्याकडे तीन किंवा त्यापेक्षा जास्त चल असल्यास, अ‍ॅरे आदर्श आहे. गुणाकार आणि जोडणीची वारंवार जोडणी वापरुन आपण पद्धतशीररित्या निराकरणात येऊ शकता.

पाऊल टाकण्यासाठी

4 पैकी भाग 1: मॅट्रिक्स रेखांकन

1. आपल्याकडे पुरेसा डेटा आहे हे सत्यापित करा. मॅट्रिक्सचा वापर करून रेषात्मक प्रणालीतील प्रत्येक चल करीता एक अद्वितीय समाधान मिळविण्यासाठी, आपण सोडवण्याचा प्रयत्न करीत असलेल्या व्हेरिएबल्सची संख्या जितकी समीकरणे आवश्यक आहेत. उदाहरणार्थ: x, y आणि z या चलांसह तुम्हाला तीन समीकरणे आवश्यक आहेत. आपल्याकडे चार चल असल्यास, आपल्याला चार समीकरणे आवश्यक आहेत.
   • आपल्याकडे व्हेरिएबल्सच्या संख्येपेक्षा कमी समीकरणे असल्यास, आपल्याला व्हेरिएबल्सच्या काही सीमा सापडतील (जसे की x = 3y आणि y = 2z), परंतु आपल्याला तंतोतंत निराकरण मिळू शकत नाही. या लेखासाठी आम्ही केवळ एका अनोख्या समाधानासाठी कार्य करू.
2. आपली समीकरणे मानक स्वरुपात लिहा. आपण समीकरणांवरील डेटा मॅट्रिक्स स्वरूपात ठेवण्यापूर्वी आपण प्रथम प्रत्येक समीकरण मानक स्वरूपात लिहा. रेषात्मक समीकरणाचे प्रमाणित रूप म्हणजे एक्स + बाय + सीझेड = डी, जेथे अपरकेस अक्षरे गुणांक (संख्या) आहेत आणि शेवटची संख्या (या उदाहरणातील डी) समान चिन्हाच्या उजवीकडे आहे.
   • आपल्याकडे अधिक व्हेरिएबल्स असल्यास, जोपर्यंत आपल्याला आवश्यक असेल तितके लाइन चालू ठेवा. उदाहरणार्थ, जर आपण सहा चलांसह सिस्टमचे निराकरण करण्याचा प्रयत्न करीत असाल तर आपला डीफॉल्ट आकार Au + Bv + Cw + Dx + Ey + Fz = G सारखा दिसेल. या लेखात आम्ही फक्त तीन व्हेरिएबल्स असलेल्या सिस्टमवर लक्ष केंद्रित करू. मोठ्या आकाशगंगेचे निराकरण करणे अगदी तशाच आहे, परंतु अधिक वेळ आणि अधिक पावले उचलतात.
   • लक्षात घ्या की प्रमाणित स्वरूपात, अटींमधील ऑपरेशन्स नेहमीच एक अतिरिक्त असतात. आपल्या समीकरणात वजाबाकी असल्यास त्याऐवजी जोडण्याऐवजी, आपल्या गुणांकला नकारात्मक बनवून नंतर यासह कार्य करावे लागेल. हे लक्षात ठेवण्यास सुलभ करण्यासाठी आपण समीकरण पुन्हा लिहू शकता आणि ऑपरेशन जोडू शकता आणि गुणांक नकारात्मक बनवू शकता. उदाहरणार्थ, आपण 3x-2y + 4z = 1 हे समीकरण 3x + (- 2y) + 4z = 1 म्हणून पुन्हा लिहू शकता.
3. मॅट्रिक्समध्ये समीकरणांच्या प्रणालीतून संख्या ठेवा. एक मॅट्रिक्स म्हणजे संख्येचा एक समूह, एका प्रकारची सारणी तयार केलेली, ज्याद्वारे आम्ही सिस्टम सोडविण्यासाठी कार्य करू. यात मुळात तेच समीकरण स्वतःसारखेच डेटा असते, परंतु एका सोप्या स्वरुपात. आपल्या समीकरणांचे मॅट्रिक्स मानक स्वरुपात बनविण्यासाठी, प्रत्येक समीकरणाचा गुणांक आणि निकाल केवळ एका ओळीत कॉपी करा आणि त्या ओळी एकमेकांच्या वरच्या बाजूस स्टॅक करा.
   • समजा आपल्याकडे एक सिस्टम आहे ज्यामध्ये 3x + y-z = 9, 2x-2y + z = -3 आणि x + y + z = 7 ही तीन समीकरणे आहेत. तुमच्या मॅट्रिक्सच्या सर्वात वरच्या रांगेत 3, 1, -1, 9 ही संख्या असेल कारण हे गुणांक आणि पहिल्या समीकरणाचे समाधान आहे. लक्षात घ्या की गुणांक नसलेली कोणतीही चल 1 ची गुणांक असेल असे गृहित धरले जाते. मॅट्रिक्सची दुसरी पंक्ती 2, -2, 1, -3 आणि तिसरी पंक्ती 1, 1, 1, 7 होते.
   • पहिल्या स्तंभात x गुणांक, दुसर्‍या क्रमांकामधील y गुणांक, तिसर्‍या क्रमांकाच्या झेड गुणांक आणि चौथ्यामध्ये द्रावणाच्या संरेखित संरेखित करणे सुनिश्चित करा. आपण मॅट्रिक्ससह कार्य पूर्ण केल्यावर, आपले समाधान लिहिताना हे स्तंभ महत्त्वपूर्ण असतील.
4. आपल्या संपूर्ण मॅट्रिक्स भोवती एक मोठे स्क्वेअर ब्रॅकेट काढा. संमेलनाद्वारे, मॅट्रिक्स पूर्ण संख्येच्या ब्लॉकच्या सभोवतालच्या स्क्वेअर ब्रॅकेट्सच्या जोडीद्वारे दर्शविला जातो. ब्रॅकेट्स कोणत्याही प्रकारे समाधानावर परिणाम करत नाहीत परंतु ते असे दर्शवित आहेत की आपण मॅट्रिक्ससह कार्य करीत आहात. मॅट्रिक्समध्ये कितीही पंक्ती आणि स्तंभ असू शकतात. या लेखात, आम्ही त्या संबद्ध आहोत हे सूचित करण्यासाठी सलग संज्ञाभोवती कंस वापरू.
5. सामान्य प्रतीकात्मकतेचा वापर. मॅट्रिकसह कार्य करीत असताना, संक्षेप आर सह पंक्ती आणि संक्षिप्त नाम असलेल्या स्तंभांचा संदर्भ घेणे सामान्य आहे. आपण विशिष्ट पंक्ती किंवा स्तंभ दर्शविण्यासाठी या अक्षरासह अंक वापरू शकता. उदाहरणार्थ, मॅट्रिक्सची पंक्ती 1 दर्शविण्यासाठी आपण आर 1 लिहू शकता. पंक्ती 2 नंतर आर 2 बनते.
   • आपण आर आणि सी च्या संयोजनाद्वारे मॅट्रिक्समधील कोणतीही विशिष्ट स्थिती दर्शवू शकता उदाहरणार्थ, दुसर्‍या रांगेत, तिसर्‍या स्तंभात एक शब्द दर्शविण्यासाठी आपण त्यास आर 2 सी 3 कॉल करू शकता.

4 पैकी भाग 2: मॅट्रिक्सद्वारे सिस्टम सोडविण्याकरिता ऑपरेशन्स शिकणे

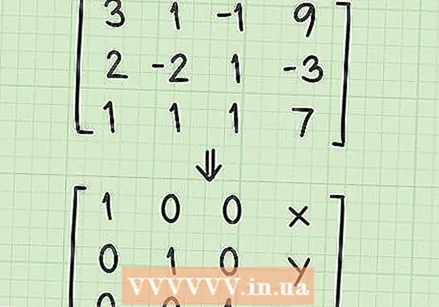1. सोल्यूशन मॅट्रिक्सचा आकार समजून घ्या. आपण आपल्या समीकरणांची प्रणाली सोडविणे सुरू करण्यापूर्वी, आपण मॅट्रिक्ससह काय करणार आहात हे समजून घेणे आवश्यक आहे. याक्षणी आपल्याकडे असे एक मॅट्रिक्स आहे:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • आपण "सोल्यूशन मॅट्रिक्स" तयार करण्यासाठी बर्‍याच मूलभूत ऑपरेशन्ससह कार्य करता. समाधान मॅट्रिक्स यासारखे दिसेल:
   • 1 0 0 x
   • 0 1 0 वाय
   • 0 0 1 झेड
   • लक्षात घ्या की मॅट्रिक्समध्ये चौथ्या स्तंभ वगळता इतर सर्व जागांमध्ये 0 च्या कर्णरेषामध्ये 1 चे असते. चौथ्या स्तंभातील संख्या म्हणजे x, y आणि z या व्हेरिएबल्सचे समाधान.
2. स्केलर गुणाकार वापरा. मॅट्रिक्स वापरुन सिस्टमचे निराकरण करण्यासाठी आपल्या विल्हेवाटचे पहिले साधन म्हणजे स्केलर गुणाकार. हे फक्त एक संज्ञा आहे याचा अर्थ असा आहे की आपण मॅट्रिक्सच्या एका रांगेत घटकांना एका संख्येने (व्हेरिएबलने नाही) ने गुणाकार करता. स्केलर गुणाकार वापरताना, लक्षात ठेवा की आपण संपूर्ण पंक्तीची प्रत्येक संज्ञा आपण निवडलेल्या कोणत्याही संख्येने गुणाकार करणे आवश्यक आहे. आपण पहिली संज्ञा विसरल्यास आणि फक्त गुणाकार केल्यास आपल्याला चुकीचे निराकरण मिळेल. तथापि, आपल्याला एकाच वेळी संपूर्ण मॅट्रिक्सची गुणाकार करण्याची आवश्यकता नाही. स्केलर गुणामध्ये आपण एकावेळी फक्त एका ओळीवर कार्य करता.
   • स्केलर गुणामध्ये अपूर्णांक वापरणे सामान्य आहे कारण आपल्याला बहुतेक वेळा 1 ची कर्णरेषा मिळवायची असते. अपूर्णांकांसह काम करण्याची सवय लावा. चुकीचे स्वरूपात आपले अंश लिहिण्यास सक्षम होण्यासाठी (मॅट्रिक्स सोडविण्याच्या बहुतेक चरणांसाठी) सोपे होईल, नंतर अंतिम समाधानासाठी त्यांना मिश्रित संख्यांमध्ये परत रूपांतरित करा. म्हणून, 1/2 क्रमांकासह कार्य करणे सोपे आहे जर आपण ते 5/3 असे लिहिले तर.
   • उदाहरणार्थ, आमच्या उदाहरणातील समस्येची पहिली पंक्ती (आर 1) [3,1, -1,9] या शब्दासह प्रारंभ होते. सोल्यूशन मॅट्रिक्समध्ये पहिल्या ओळीच्या पहिल्या स्थानावर 1 असणे आवश्यक आहे. 3 ते 1 मध्ये "बदलण्यासाठी" आपण संपूर्ण पंक्ती 1/3 ने गुणाकार करू शकतो. हे [1,1 / 3, -1 / 3,3] चे नवीन आर 1 तयार करते.
   • ते जेथे असतील तेथे कोणतीही नकारात्मक चिन्हे सोडण्याची खात्री करा.
3. पंक्ती जोडणे किंवा पंक्तीचे वजाबाकी वापरा. आपण वापरू शकता असे दुसरे साधन म्हणजे मॅट्रिक्सच्या दोन ओळी जोडणे किंवा वजा करणे. आपल्या सोल्यूशन मॅट्रिक्समध्ये 0 अटी तयार करण्यासाठी, 0 वर जाण्यासाठी आपल्याला संख्या जोडा किंवा वजा कराव्या लागतील. उदाहरणार्थ, जर आर 1 मॅट्रिक्सचा असेल [1,4,3,2] आणि आर 2 [1,3,5,8] असेल तर आपण दुसर्‍या पंक्तीमधून प्रथम पंक्ती वजा करू आणि नवीन पंक्ती तयार करू शकता [0, -1, 2.6], कारण 1-1 = 0 (प्रथम स्तंभ), 3-4 = -1 (दुसरा स्तंभ), 5-3 = 2 (तृतीय स्तंभ) आणि 8-2 = 6 (चौथा स्तंभ). पंक्ती जोडणे किंवा पंक्तीचे वजाबाकी करीत असताना आपण प्रारंभ केलेल्या पंक्तीऐवजी आपला नवीन परिणाम पुन्हा लिहा. या प्रकरणात आम्ही पंक्ती 2 काढू आणि नवीन पंक्ती [0, -1,2,6] समाविष्ट करू.
   • आपण शॉर्टहँड नोटेशन वापरू शकता आणि ही क्रिया आर 2-आर 1 = [0, -1,2,6] म्हणून घोषित करू शकता.
   • लक्षात ठेवा की जोड आणि वजाबाकी समान कार्याचे अगदी विरुद्ध प्रकार आहेत. दोन संख्या जोडणे किंवा त्यास उलट वजा करणे विचार करा. उदाहरणार्थ, आपण 3-3 = 0 साध्या समीकरणापासून प्रारंभ केल्यास आपण यास 3 + (- 3) = 0 ची जोड समस्या म्हणून विचार करू शकता. निकाल तोच आहे. हे सोपे दिसते, परंतु काहीवेळा एखाद्या स्वरूपात किंवा दुसर्‍या स्वरूपात समस्येवर विचार करणे कधीकधी सोपे होते. फक्त आपल्या नकारात्मक चिन्हेंवर लक्ष ठेवा.
4. एका चरणात पंक्ती जोड आणि स्केलर गुणाकार एकत्र करा. आपण अटी नेहमी जुळतील अशी अपेक्षा करू शकत नाही, म्हणून आपण आपल्या मॅट्रिक्समध्ये 0 तयार करण्यासाठी एक साधा जोड किंवा वजाबाकी वापरू शकता. बर्‍याचदा आपल्याला दुसर्‍या ओळीतून एकाधिक (किंवा वजा करणे) करावे लागेल. हे करण्यासाठी, आपण प्रथम स्केलर गुणाकार करा, नंतर आपण बदलू इच्छित असलेल्या लक्ष्य पंक्तीमध्ये तो परिणाम जोडा.
   • समजा; की [1,1,2,6] पैकी एक पंक्ती 1 आणि [2,3,1,1] पैकी एक पंक्ती 2 आहे. आपल्याला आर 2 च्या पहिल्या स्तंभात 0 संज्ञा पाहिजे आहे. म्हणजेच, आपल्याला 2 मध्ये बदलून 0 करायचे आहे. हे करण्यासाठी आपल्याला 2 वजा करणे आवश्यक आहे. स्केलर गुणाकार 2 ने प्रथम पंक्ती 1 गुणाकार करून आपण 2 मिळवू शकता आणि नंतर दुसर्‍या पंक्तीमधून प्रथम पंक्ती वजा करू शकता. थोडक्यात हे आर 2-2 * * आर 1 म्हणून लिहिले जाऊ शकते. प्रथम, [2,2,4,12] मिळविण्यासाठी आर 1 ला 2 ने गुणाकार करा. नंतर [2 (2-2), (3-2), (1-4), (1-12)] मिळविण्यासाठी हे आर 2 वजा करा. हे सुलभ करा आणि आपले नवीन आर 2 [0,1, -3, -11] असतील.
5. आपण कार्य करता तसाच बदल न करता राहिलेल्या पंक्ती कॉपी करा. आपण मॅट्रिक्सवर काम करता तेव्हा आपण एकाच वेळी एकल पंक्ती बदलू, एकतर स्केलर गुणाकार, पंक्ती जोडणे किंवा पंक्ती वजाबाकी किंवा चरणांचे संयोजन. आपण एक पंक्ती बदलता तेव्हा आपल्या मॅट्रिक्सच्या इतर पंक्ती त्यांच्या मूळ स्वरुपात कॉपी केल्याचे सुनिश्चित करा.
   • एकत्रित गुणाकार आणि एका हालचालीत जोडणे यासाठी एक सामान्य त्रुटी उद्भवते. उदाहरणार्थ, म्हणा की आपल्याला आर 2 वरून दोनदा वजा करणे आवश्यक आहे. ही पद्धत करण्यासाठी जेव्हा आपण आर 1 ला 2 ने गुणाकार करता तेव्हा लक्षात ठेवा की आर 1 मॅट्रिक्समध्ये बदलत नाही. आपण केवळ आर 2 बदलण्यासाठी गुणाकार करता. प्रथम आर 1 त्याच्या मूळ स्वरुपात कॉपी करा, नंतर आर 2 मध्ये बदल करा.
6. प्रथम वरपासून खालपर्यंत काम करा. सिस्टमचे निराकरण करण्यासाठी, आपण एका अतिशय संयोजित पद्धतीने कार्य करता, एका वेळी मॅट्रिक्सची एक संज्ञा अनिवार्यपणे "निराकरण" करतात. तीन-व्हेरिएबल अ‍ॅरेसाठी क्रम यासारखे दिसेल:
   • 1. पहिल्या पंक्तीमध्ये प्रथम 1 बनवा, प्रथम स्तंभ (आर 1 सी 1).
   • 2. दुसर्‍या रांगेत 0 करा, प्रथम स्तंभ (आर 2 सी 1).
   • 3. दुसर्‍या रांगेत एक 1 बनवा, दुसरा स्तंभ (आर 2 सी 2).
   • 4. तिसर्‍या रांगेत 0 बनवा, प्रथम स्तंभ (आर 3 सी 1).
   • 5. तिसर्‍या रांगेत 0 बनवा, दुसरा स्तंभ (आर 3 सी 2).
   • 6. तिसर्‍या रांगेत एक 1 बनवा, तिसरा स्तंभ (आर 3 सी 3).
7. खालपासून वरपर्यंत परत काम करा. या क्षणी, आपण चरण योग्यरित्या केले असल्यास, आपण निराकरण अर्ध्या मार्गाने आहात. आपल्याकडे 0 च्या कर्णरेषा खाली असणे आवश्यक आहे. चौथ्या स्तंभातील संख्या या क्षणी काही फरक पडत नाही. आता आपण खालीलप्रमाणे शीर्षस्थानी परत कार्य करा:
   • दुसर्‍या रांगेत 0 तयार करा, तिसरा कॉलम (R2C3).
   • पहिल्या पंक्तीमध्ये एक 0 तयार करा, तिसरा स्तंभ (R1C3).
   • पहिल्या रांगेत 0 तयार करा, दुसरा स्तंभ (R1C2).
8. आपण समाधान मॅट्रिक्स तयार केला आहे का ते तपासा. जर आपले कार्य योग्य असेल तर आपण प्रथम तीन स्तंभांच्या इतर स्थानांवर आर 1 सी 1, आर 2 सी 2, आर 3 सी 3 आणि 0 च्या कर्णरेषामध्ये 1 च्या द्रावणासह मैट्रिक्स तयार केला आहे. चौथ्या स्तंभातील संख्या आपल्या रेखीय प्रणालीसाठीचे निराकरण आहेत.

4 पैकी भाग 3: आकाशगंगाचे निराकरण करण्यासाठी चरण विलीन करा

1. रेखीय समीकरणांच्या उदाहरणासह प्रारंभ करा. या चरणांचा सराव करण्यासाठी, आपण यापूर्वी वापरलेल्या सिस्टीमसह प्रारंभ करूया: 3x + y-z = 9, 2x-2y + z = -3, आणि x + y + z = 7. आपण हे मॅट्रिक्समध्ये लिहित असल्यास, आपल्याकडे आर 1 = [3,1, -1,9], आर 2 = [2, -2,1, -3] आणि आर 3 = [1,1,1,7] आहेत.
2. प्रथम स्थानावर आर 1 सी 1 मध्ये 1 तयार करा. लक्षात घ्या की आर 1 या टप्प्यावर प्रारंभ होतो. आपल्याला ते 1 मध्ये बदलावे लागेल. आपण हे स्केलर गुणाकाराने करू शकता, आर 1 ची सर्व चार श्रेणी 1/3 ने गुणाकार करू शकता. शॉर्टहँड मध्ये आपण आर 1 * * 1/3 म्हणून लिहू शकता. हे आर 1 = [1,1 / 3, -1 / 3,3] असल्यास आर 1 साठी एक नवीन निकाल देते. आर 2 = [2, -2,1, -3] आणि आर 3 = [1,1,1,7] तेव्हा बदललेले, आर 2 आणि आर 2 कॉपी करा.
   • लक्षात घ्या की गुणाकार आणि विभागणी केवळ एकमेकांची व्यस्त कार्ये आहेत. आपण असे म्हणू शकतो की निकाल न बदलता आपण 1/3 किंवा 3 ने गुणाकार करू.
3. दुसर्‍या रांगेत 0 तयार करा, प्रथम स्तंभ (R2C1). या टप्प्यावर, आर 2 = [2, -2,1, -3]. सोल्यूशन मॅट्रिक्सच्या जवळ जाण्यासाठी, आपल्याला प्रथम टर्म 2 वरून 0 पर्यंत बदलण्याची आवश्यकता आहे. आर 1 ने 1 सह आरंभ केल्यापासून आपण आर 1 चे मूल्य दोनदा वजा करून हे करू शकता. शॉर्टहँडमध्ये, ऑपरेशन आर 2- 2 * आर 1 लक्षात ठेवा, आपण आर 1 बदलत नाही, त्यासह कार्य करा. तर आर 1 असल्यास प्रथम आर 1 = [1,1 / 3, -1 / 3,3] कॉपी करा. नंतर आपण आर 1 ची प्रत्येक मुदत दुप्पट केल्यास आपल्यास 2 * आर 1 = [2,2 / 3, -2 / 3,6] मिळेल. शेवटी, आपला नवीन आर 2 मिळविण्यासाठी हा परिणाम मूळ आर 2 वजा करा. टर्मनुसार कार्य करणे, हा वजाबाकी (2-2), (-2-2 / 3), (1 - (2/3)), (-3-6) होते. आम्ही नवीन आर 2 = [0, -8 / 3,5 / 3, -9] वर हे सुलभ करतो. लक्षात ठेवा की प्रथम टर्म 0 आहे (आपले लक्ष्य जे होते).
   • R3 = [1,1,1,7] म्हणून पंक्ती 3 (जे बदलली नाही) लिहा.
   • चिन्हे योग्य राहतील याची खात्री करण्यासाठी नकारात्मक संख्या वजा करताना सावधगिरी बाळगा.
   • आता प्रथम अपूर्णांक त्यांच्या अयोग्य फॉर्ममध्ये टाकू. हे सोल्यूशन नंतरचे चरण सुलभ करते. आपण समस्येच्या शेवटच्या चरणात अपूर्णांक सुलभ करू शकता.
4. दुसर्‍या रांगेत एक 1 तयार करा, दुसरा स्तंभ (R2C2). 1 च्या कर्णरेषा तयार करणे सुरू ठेवण्यासाठी, आपण द्वितीय टर्म -8/3 मध्ये 1 मध्ये रुपांतरित केले पाहिजे. त्या संख्येच्या परस्परसंबंधाने संपूर्ण पंक्ती गुणाकार करुन (-3/8) करा. प्रतीकात्मकरित्या, ही पायरी आर 2 * आहे (- 3/8). परिणामी दुसरी पंक्ती आर 2 = [0.1, -5 / 8.27 / 8] आहे.
   • लक्षात घ्या की जर पंक्तीचा डावा अर्धा भाग 0 आणि 1 सह समाधानास सामोरे जाऊ लागला तर उजवा अर्धा अयोग्य अपूर्णांकांसह कुरुप दिसू शकेल. ते आता त्यांच्यासाठी फक्त त्यांनाच सोडा.
   • अस्पृश्य पंक्तीची प्रतिलिपी सुरू ठेवण्यास विसरू नका, तर आर 1 = [1,1 / 3, -1 / 3,3] आणि आर 3 = [1,1,1,7].
5. तिसर्‍या रांगेत 0 तयार करा, प्रथम स्तंभ (R3C1). आपले लक्ष आता तिसर्‍या पंक्तीकडे जाईल, आर 3 = [1,1,1,7]. प्रथम स्थानावर 0 करण्यासाठी, आपण त्या स्थितीत सध्या 1 वरुन 1 वजा करणे आवश्यक आहे. आपण वर पाहिले तर, आर 1 च्या पहिल्या स्थानावर 1 आहे. आपल्याला आवश्यक असलेला निकाल मिळविण्यासाठी आपल्याला फक्त आर 3 वरून आर 1 वजा करणे आवश्यक आहे. टर्मसाठी कार्यरत मुदत, ही (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3) होते. नंतर या चार मिनी-समस्या नवीन आर 3 = [0.2 / 3.4 / 3.4] वर सरलीकृत केल्या जाऊ शकतात.
   • आर 1 = [1.1 / 3, -1 / 3.3] आणि आर 2 = [0.1, -5 / 8.27 / 8] वर कॉपी करणे सुरू ठेवा. लक्षात ठेवा आपण एका वेळी फक्त एक पंक्ती बदलली आहे.
6. तिसर्‍या रांगेत 0 बनवा, दुसरा स्तंभ (R3C2). हे मूल्य सध्या 2/3 आहे, परंतु ते 0 मध्ये रूपांतरित केले जाणे आवश्यक आहे. पहिल्या दृष्टीक्षेपात असे दिसते आहे की आपण आर 1 च्या मूल्यांना दुप्पट वजा करू शकता, कारण आर 1 च्या संबंधित स्तंभात 1/3 आहे. तथापि, आपण आर 1 ची सर्व मूल्ये दुप्पट व वजा केल्यास, आर 3 च्या पहिल्या स्तंभातील 0 0 बदलत आहेत, जे आपल्याला नको आहेत. आपल्या निराकरणात हे एक पाऊल मागे असेल. तर आपल्याला आर 2 च्या काही संयोजनासह कार्य करावे लागेल. आर 2 वरून 2/3 वजा करणे प्रथम स्तंभ न बदलता दुसर्‍या स्तंभात 0 तयार करते. थोडक्यात हे आर 3-2 / 3 * आर 2 आहे. वैयक्तिक अटी (0-0), (2 / 3-2 / 3), (4/3 - (- 5/3 * 2/3)), (4-27 / 8 * 2/3) . सरलीकरण नंतर आर 3 = [0,0,42 / 24,42 / 24] देते.
7. तिसर्‍या रांगेत एक 1 तयार करा, तिसरा स्तंभ (R3C3). ज्या संख्येने म्हटले आहे त्यानुसार हे एक साधे गुणाकार आहे. सध्याचे मूल्य /२/२. आहे, म्हणून आपणास हवे असलेले मूल्य मिळविण्यासाठी आपण 24/42 ने गुणाकार करू शकता. लक्षात घ्या की प्रथम दोन संज्ञा दोन्ही 0 आहेत, म्हणून कोणतीही गुणाकार 0 राहते. आर 3 चे नवीन मूल्य = [0,0,1,1].
   • लक्षात घ्या की मागील चरणात बर्‍याच गुंतागुंत वाटणारे अपूर्णांक आधीच निराकरण करण्यास सुरवात करत आहेत.
   • आर 1 = [1.1 / 3, -1 / 3.3] आणि आर 2 = [0.1, -5 / 8.27 / 8] वर सुरू ठेवा.
   • लक्षात घ्या की याक्षणी आपल्या सोल्यूशन मॅट्रिक्ससाठी आपल्याकडे 1 चे कर्ण आहे. आपला समाधान शोधण्यासाठी आपल्याला केवळ मॅट्रिक्सचे तीन घटक 0s मध्ये रूपांतरित करावे लागतील.
8. तिसर्‍या स्तंभातील दुसर्‍या रांगेत 0 तयार करा. तिसर्‍या स्तंभात -5/8 च्या मूल्यासह, आर 2 सध्या [0.1, -5 / 8.27 / 8] आहे. आपणास त्याचे बदल ०.० वर करावे लागेल. याचा अर्थ असा आहे की आपल्याला आर 3 सह काही ऑपरेशन करावे लागेल ज्यामध्ये 5/8 जोडणे असेल. आर 3 चा संबंधित तिसरा स्तंभ 1 असल्यामुळे आपण आर 3 ची सर्व मूल्ये 5/8 ने गुणाकार करुन निकाल आर 2 मध्ये जोडणे आवश्यक आहे. थोडक्यात हे आर 2 + 5/8 * आर 3 आहे. टर्मसाठीची मुदत ही आर 2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8) आहे. हे आर 2 = [0,1,0,4] वर सरलीकृत केले जाऊ शकते.
   • नंतर आर 1 = [1,1 / 3, -1 / 3,3] आणि आर 3 = [0,0,1,1] कॉपी करा.
9. पहिल्या पंक्तीमध्ये एक 0 तयार करा, तिसरा स्तंभ (R1C3). प्रथम पंक्ती सध्या आर 1 = [1,1 / 3, -1 / 3,3] आहे. आपल्याला R3 चे काही संयोजन वापरून तिसर्‍या स्तंभातील -1/3 0 मध्ये रूपांतरित करावे लागेल. आपल्याला आर 2 वापरायचा नाही, कारण आर 2 च्या दुसर्‍या स्तंभातील 1 आर 1 ला चुकीचा मार्ग बदलेल. तर आपण आर 3 * * 1/3 गुणाकार करा आणि निकाल आर 1 मध्ये जोडा. यासाठी संकेतक आर 1 + 1/3 * आर 3 आहे. टर्म विस्ताराच्या संज्ञेचा परिणाम आर 1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3) मध्ये होतो. आपण हे नवीन आर 1 = [1,1 / 3,0,10 / 3] वर सरलीकृत करू शकता.
   • न बदललेले आर 2 = [0,1,0,4] आणि आर 3 = [0,0,1,1] कॉपी करा.
10. पहिल्या पंक्तीमध्ये दुसरे स्तंभ (आर 1 सी 2) 0 बनवा. जर सर्व काही योग्य प्रकारे केले गेले असेल तर ही शेवटची पायरी असावी. आपल्याला दुसर्‍या स्तंभातील 1/3 ला 0 मध्ये रुपांतरीत करावे लागेल. आपण हे आर 2 = * 1/3 गुणाकार आणि वजा करून मिळवू शकता. थोडक्यात, हे आर 1-1 / 3 * आर 2 आहे. परिणाम आर 1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3) आहे. सरलीकरण नंतर आर 1 = [1,0,0,2] देते.
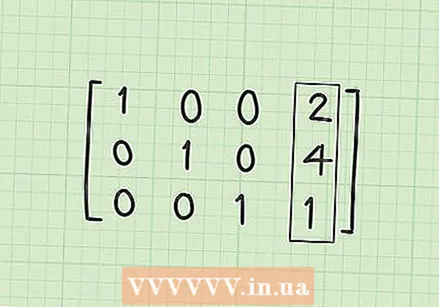11. सोल्यूशन मॅट्रिक्सचा शोध घ्या. या टप्प्यावर, जर सर्व काही ठीक झाले तर आपल्याकडे आर 1 = [1,0,0,2], आर 2 = [0,1,0,4] आणि आर 3 = [0,0,1,1] आहेत. असणे आवश्यक आहे. लक्षात घ्या की आपण हे ब्लॉक मॅट्रिक्स फॉर्ममध्ये एका ओळीच्या वर असलेल्या ओळींसह लिहिले तर आपल्याकडे 0 च्या पुढील कर्ण 1 आहे आणि आपले निराकरण चौथ्या स्तंभात आहे. समाधान मॅट्रिक्स यासारखे दिसले पाहिजे:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. आपले समाधान समजून घेत आहे. रेषात्मक समीकरणे मॅट्रिक्समध्ये रुपांतरित केल्यावर, आपण पहिल्या स्तंभात x गुणांक ठेवले, दुसर्‍या स्तंभात वाई गुणांक, तिसर्‍या स्तंभात झेड गुणांक ठेवले. जर आपल्याला मॅट्रिक्स पुन्हा समीकरणांवर पुन्हा लिहायचे असेल तर, मॅट्रिक्सच्या या तीन ओळींचा अर्थ 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 आणि 0x + 0y + 1z = 1 ही तीन समीकरणे आहेत. आपण 0 संज्ञांचा पार करू शकतो आणि 1 गुणांक लिहू नये म्हणून, ही तीन समीकरणे सोल्यूशनमध्ये x = 2, y = 4, आणि z = 1 सुलभ करते. हे आपल्या रेषीय समीकरणांच्या सिस्टमचे निराकरण आहे.

4 चे भाग 4: आपले समाधान शोधत आहे

1. प्रत्येक समीकरणातील प्रत्येक चलमधील समाधानाचा समावेश करा. आपला समाधान प्रत्यक्षात योग्य आहे याची तपासणी करणे नेहमीच चांगली कल्पना आहे. आपण हे आपल्या मूळ परीणामांच्या परीक्षेच्या चाचणीद्वारे करता.
   • या समस्येचे मूळ समीकरणे अशी: 3x + y-z = 9, 2x-2y + z = -3 आणि x + y + z = 7. जेव्हा आपण व्हेरिएबल्स आपल्याला त्यांच्या मूल्यांसह पुनर्स्थित करता तेव्हा आपल्याला 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 आणि 2 + 4 + 1 = 7 मिळतात.
2. कोणतीही तुलना सोपी करा. ऑपरेशन्सच्या मूलभूत नियमांनुसार प्रत्येक समीकरणात ऑपरेशन्स करा. पहिले समीकरण 6 + 4-1 = 9 किंवा 9 = 9 वर सरलीकृत होते. दुसरे समीकरण 4-8 + 1 = -3, किंवा -3 = -3 मध्ये सुलभ केले जाऊ शकते. शेवटचे समीकरण फक्त 7 = 7 आहे.
   • कोणतेही समीकरण खरे गणिताच्या विधानास सुलभ करते म्हणून आपले निराकरण योग्य आहे. जर कोणतेही निराकरण चुकीचे असेल तर आपले कार्य पुन्हा तपासा आणि कोणत्याही त्रुटी पहा. वाटेत वजा चिन्हे दूर केल्यावर किंवा गुणाकार आणि अपूर्णांकांची भर घालताना काही सामान्य चुका उद्भवतात.
3. आपले अंतिम निराकरण लिहा. या दिलेल्या समस्येसाठी, अंतिम समाधान x = 2, y = 4 आणि झेड = 1 आहे.

टिपा

• जर आपली समीकरण प्रणाली बर्‍याच व्हेरिएबल्ससह खूप जटिल असेल तर आपण हातांनी कार्य करण्याऐवजी ग्राफिंग कॅल्क्युलेटर वापरण्यास सक्षम होऊ शकता. याविषयी माहितीसाठी तुम्ही विकीचा सल्ला घेऊ शकता.