सामग्री

• पावले
• 3 पैकी 1 पद्धत: स्थिर मुदतीशिवाय क्यूबिक समीकरण कसे सोडवायचे
• 3 पैकी 2 पद्धत: मल्टीप्लायर्स वापरून संपूर्ण मुळे कशी शोधायची
• 3 पैकी 3 पद्धत: भेदभाव वापरून समीकरण कसे सोडवायचे

क्यूबिक समीकरणात, सर्वात जास्त घातांक 3 आहे, अशा समीकरणाला 3 मुळे (उपाय) असतात आणि त्याचे स्वरूप असते ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... काही क्यूबिक समीकरणे सोडवणे इतके सोपे नाही, परंतु जर तुम्ही योग्य पद्धत (चांगल्या सैद्धांतिक पार्श्वभूमीसह) लागू केलीत, तर तुम्हाला अगदी गुंतागुंतीच्या क्यूबिक समीकरणाची मुळे सापडतील - यासाठी चतुर्भुज समीकरण सोडवण्यासाठी सूत्र वापरा, शोधा संपूर्ण मुळे, किंवा भेदभावाची गणना करा.

पावले

3 पैकी 1 पद्धत: स्थिर मुदतीशिवाय क्यूबिक समीकरण कसे सोडवायचे

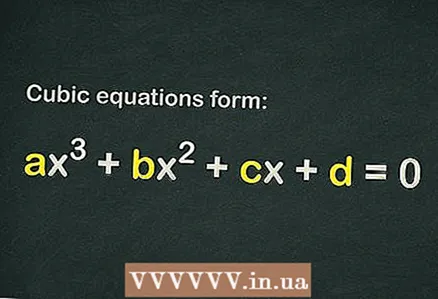1. 1 क्यूबिक समीकरणात विनामूल्य पद आहे का ते शोधा d{ displaystyle d}. क्यूबिक समीकरणाला फॉर्म आहे ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... एक समीकरण क्यूबिक मानले जाण्यासाठी, फक्त संज्ञा पुरेसे आहे ${ displaystyle x ^ {3}}$ (म्हणजे, इतर कोणतेही सदस्य असू शकत नाहीत).
   • जर समीकरणाला विनामूल्य पद असेल ${ displaystyle d}$, वेगळी पद्धत वापरा.
   • जर समीकरणात ${ displaystyle a = 0}$, तो क्यूबिक नाही.
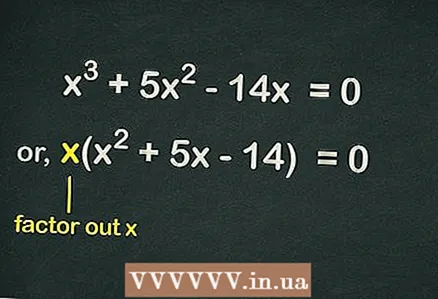2. 2 कंसातून बाहेर काढा x{ displaystyle x}. समीकरणात कोणतेही विनामूल्य पद नसल्यामुळे, समीकरणातील प्रत्येक संज्ञेत चल समाविष्ट आहे ${ displaystyle x}$... याचा अर्थ असा की एक ${ displaystyle x}$ समीकरण सुलभ करण्यासाठी कंसातून वगळले जाऊ शकते. अशा प्रकारे, समीकरण असे लिहिले जाईल: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • उदाहरणार्थ, क्यूबिक समीकरण दिले ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • बाहेर काढा ${ displaystyle x}$ कंस आणि मिळवा ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
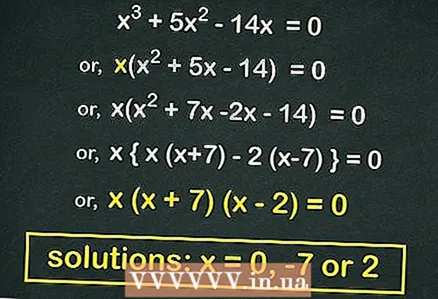3. 3 घटक (दोन द्विपदांचे उत्पादन) द्विघात समीकरण (शक्य असल्यास). स्वरूपाची अनेक द्विघात समीकरणे ${ displaystyle ax ^ {2} + bx + c = 0}$ गुणांकित केले जाऊ शकते. जर आपण बाहेर काढले तर असे समीकरण चालू होईल ${ displaystyle x}$ कंस बाहेर. आमच्या उदाहरणात:
   • कंसातून बाहेर काढा ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • द्विघात समीकरण काढा: ${ displaystyle x (x + 7) (x-2) = 0}$
   • प्रत्येक बिन समान करा ${ प्रदर्शन शैली 0}$... या समीकरणाची मुळे आहेत ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 एक विशेष सूत्र वापरून चतुर्भुज समीकरण सोडवा. चतुर्भुज समीकरण गुणन करू शकत नसल्यास हे करा. समीकरणाची दोन मुळे शोधण्यासाठी, गुणांकांची मूल्ये ${ प्रदर्शन शैली a}$, ${ displaystyle b}$, ${ प्रदर्शन शैली c}$ सूत्र मध्ये पर्याय ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • आमच्या उदाहरणात, गुणांकांची मूल्ये बदला ${ प्रदर्शन शैली a}$, ${ displaystyle b}$, ${ प्रदर्शन शैली c}$ (${ प्रदर्शन शैली 3}$, ${ displaystyle -2}$, ${ प्रदर्शन शैली 14}$) सूत्रात:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ प्रदर्शन शैली { frac {- (- 2) pm { sqrt {((-2) {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ प्रदर्शन शैली { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • पहिले मूळ:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • दुसरे मूळ:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 क्यूबिक समीकरणावर उपाय म्हणून शून्य आणि चतुर्भुज मुळे वापरा. द्विघात समीकरणांना दोन मुळे असतात, तर क्यूबिकमध्ये तीन असतात. आपल्याला आधीच दोन उपाय सापडले आहेत - ही चतुर्भुज समीकरणाची मुळे आहेत. जर तुम्ही "x" कंसांच्या बाहेर ठेवले तर तिसरे समाधान होईल ${ प्रदर्शन शैली 0}$.
   • जर तुम्ही कंसातून "x" काढले तर तुम्हाला मिळेल ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, म्हणजे, दोन घटक: ${ displaystyle x}$ आणि कंसातील चतुर्भुज समीकरण. यापैकी कोणतेही घटक असल्यास ${ प्रदर्शन शैली 0}$, संपूर्ण समीकरण देखील समान आहे ${ प्रदर्शन शैली 0}$.
   • अशा प्रकारे, द्विघात समीकरणाची दोन मुळे म्हणजे घन समीकरणाचे समाधान. तिसरा उपाय आहे ${ displaystyle x = 0}$.

3 पैकी 2 पद्धत: मल्टीप्लायर्स वापरून संपूर्ण मुळे कशी शोधायची

1. 1 क्यूबिक समीकरणात विनामूल्य पद असल्याची खात्री करा d{ displaystyle d}. जर फॉर्मच्या समीकरणात ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ एक विनामूल्य सदस्य आहे ${ displaystyle d}$ (जे शून्याच्या बरोबरीचे नाही), कंस बाहेर "x" लावण्याचे काम करणार नाही. या प्रकरणात, या विभागात वर्णन केलेली पद्धत वापरा.
   • उदाहरणार्थ, क्यूबिक समीकरण दिले ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... समीकरणाच्या उजव्या बाजूला शून्य मिळवण्यासाठी, जोडा ${ प्रदर्शन शैली 6}$ समीकरणाच्या दोन्ही बाजूंना.
   • समीकरण चालू होईल ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... म्हणून ${ displaystyle d = 6}$, पहिल्या विभागात वर्णन केलेली पद्धत वापरली जाऊ शकत नाही.
2. 2 गुणांकाचे घटक लिहा अ{ प्रदर्शन शैली a} आणि एक विनामूल्य सदस्य d{ displaystyle d}. म्हणजेच, संख्येचे घटक शोधा ${ displaystyle x ^ {3}}$ आणि समान चिन्हापूर्वी संख्या. लक्षात ठेवा की एका संख्येचे गुणक ही संख्या आहेत जी, गुणाकार केल्यावर, ती संख्या तयार करतात.
   • उदाहरणार्थ, नंबर मिळवण्यासाठी 6, आपल्याला गुणाकार करणे आवश्यक आहे ${ प्रदर्शन शैली 6 वेळा 1}$ आणि ${ प्रदर्शन शैली 2 वेळा 3}$... तर संख्या 1, 2, 3, 6 संख्येचे घटक आहेत 6.
   • आमच्या समीकरणात ${ displaystyle a = 2}$ आणि ${ displaystyle d = 6}$... गुणक 2 आहेत 1 आणि 2... गुणक 6 संख्या आहेत 1, 2, 3 आणि 6.
3. 3 प्रत्येक घटक विभाजित करा अ{ प्रदर्शन शैली a} प्रत्येक घटकासाठी d{ displaystyle d}. परिणामी, तुम्हाला भरपूर अंश आणि अनेक पूर्णांक मिळतात; क्यूबिक समीकरणाची मुळे पूर्णांकांपैकी एक किंवा पूर्णांकांपैकी एकचे नकारात्मक मूल्य असेल.
   • आमच्या उदाहरणात, घटक विभाजित करा ${ प्रदर्शन शैली a}$ (1 आणि 2) घटकांद्वारे ${ displaystyle d}$ (1, 2, 3 आणि 6). तुम्हाला मिळेल: ${ प्रदर्शन शैली 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ प्रदर्शन शैली 2}$ आणि ${ displaystyle { frac {2} {3}}}$... आता या सूचीमध्ये प्राप्त अपूर्णांक आणि संख्यांची नकारात्मक मूल्ये जोडा: ${ प्रदर्शन शैली 1}$, ${ प्रदर्शन शैली -1}$, ${ displaystyle { frac {1} {2}}}$, ${ प्रदर्शन शैली - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ प्रदर्शन शैली - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ प्रदर्शन शैली - { frac {1} {6}}}$, ${ प्रदर्शन शैली 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ आणि ${ प्रदर्शन शैली - { frac {2} {3}}}$... क्यूबिक समीकरणाची संपूर्ण मुळे या सूचीतील काही संख्या आहेत.
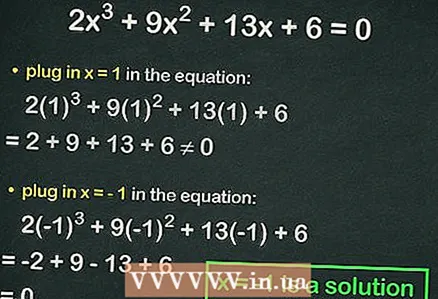4. 4 क्यूबिक समीकरण मध्ये पूर्णांक प्लग करा. जर समानता खरी असेल तर, प्रतिस्थापित संख्या समीकरणाचे मूळ आहे. उदाहरणार्थ, समीकरण मध्ये पर्याय ${ प्रदर्शन शैली 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ प्रदर्शन शैली 2 + 9 + 13 + 6}$ ≠ 0, म्हणजे समानता पाळली जात नाही. या प्रकरणात, पुढील नंबर प्लग करा.
   • पर्याय ${ प्रदर्शन शैली -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. अशा प्रकारे, ${ प्रदर्शन शैली -1}$ समीकरणाचे संपूर्ण मूळ आहे.
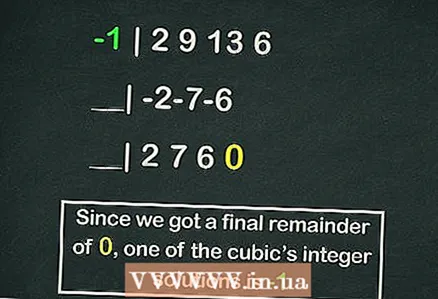5. 5 द्वारे बहुपदी विभाजित करण्याची पद्धत वापरा हॉर्नरची योजनासमीकरणाची मुळे जलद शोधण्यासाठी. जर तुम्हाला समीकरणांमध्ये संख्या स्वहस्ते बदलण्याची इच्छा नसेल तर हे करा. हॉर्नर स्कीममध्ये, पूर्णांक समीकरणाच्या गुणांकांच्या मूल्यांनी विभागले जातात ${ प्रदर्शन शैली a}$, ${ displaystyle b}$, ${ प्रदर्शन शैली c}$ आणि ${ displaystyle d}$... जर संख्या समान प्रमाणात विभागली जाऊ शकते (म्हणजे, उर्वरित आहे ${ प्रदर्शन शैली 0}$), पूर्णांक हे समीकरणाचे मूळ आहे.
   • हॉर्नर योजना वेगळ्या लेखास पात्र आहे, परंतु या योजनेचा वापर करून आमच्या क्यूबिक समीकरणाच्या मुळांपैकी एकाची गणना करण्याचे उदाहरण खालीलप्रमाणे आहे:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • तर उर्वरित आहे ${ प्रदर्शन शैली 0}$, परंतु ${ प्रदर्शन शैली -1}$ समीकरणाच्या मुळांपैकी एक आहे.

3 पैकी 3 पद्धत: भेदभाव वापरून समीकरण कसे सोडवायचे

1. 1 समीकरणाच्या गुणांकांची मूल्ये लिहा अ{ प्रदर्शन शैली a}, ब{ displaystyle b}, c{ प्रदर्शन शैली c} आणि d{ displaystyle d}. भविष्यात गोंधळ होऊ नये म्हणून आम्ही सूचित केलेल्या गुणांकांची मूल्ये आगाऊ लिहून घेण्याची शिफारस करतो.
   • उदाहरणार्थ, समीकरण दिले ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... लिहा ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ आणि ${ displaystyle d = -1}$... आधी असेल तर ते आठवा ${ displaystyle x}$ कोणतीही संख्या नाही, संबंधित गुणांक अद्याप अस्तित्वात आहे आणि समान आहे ${ प्रदर्शन शैली 1}$.
2. 2 विशेष सूत्र वापरून शून्य भेदभावाची गणना करा. भेदक वापरून क्यूबिक समीकरण सोडवण्यासाठी, आपल्याला अनेक कठीण गणना करणे आवश्यक आहे, परंतु जर आपण सर्व चरण योग्यरित्या केले तर ही पद्धत सर्वात जटिल घन समीकरणे सोडवण्यासाठी अपरिहार्य होईल. प्रथम गणना ${ displaystyle Delta _ {0}}$ (शून्य भेदभाव) हे आपल्याला आवश्यक असलेले पहिले मूल्य आहे; हे करण्यासाठी, सूत्रातील संबंधित मूल्यांची जागा घ्या ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • भेदभाव करणारी एक संख्या आहे जी बहुपदीच्या मुळांना दर्शवते (उदाहरणार्थ, चतुर्भुज समीकरणाचा भेदभाव सूत्रानुसार मोजला जातो ${ displaystyle b ^ {2} -4ac}$).
   • आमच्या समीकरणात:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ प्रदर्शन शैली 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 सूत्र वापरून पहिल्या भेदभावाची गणना करा Δ1=2ब3−9अबc+27अ2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. प्रथम भेदभाव करणारा ${ displaystyle Delta _ {1}}$ - हे दुसरे महत्वाचे मूल्य आहे; त्याची गणना करण्यासाठी, संबंधित मूल्य निर्दिष्ट सूत्रात प्लग करा.
   • आमच्या समीकरणात:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 गणना करा:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... म्हणजेच, प्राप्त मूल्यांद्वारे घन समीकरणाचा भेदभाव शोधा ${ displaystyle Delta _ {0}}$ आणि ${ displaystyle Delta _ {1}}$... क्यूबिक समीकरणाचा भेदभाव सकारात्मक असल्यास, समीकरणाची तीन मुळे आहेत; जर भेदभाव शून्य असेल तर समीकरणाची एक किंवा दोन मुळे आहेत; जर भेदभाव करणारा नकारात्मक असेल तर समीकरणाचे एक मूळ आहे.
   • क्यूबिक समीकरणात नेहमी किमान एक मूळ असते, कारण या समीकरणाचा आलेख किमान एका बिंदूवर X- अक्षांना छेदतो.
   • आमच्या समीकरणात ${ displaystyle Delta _ {0}}$ आणि ${ displaystyle Delta _ {1}}$ समान आहेत ${ प्रदर्शन शैली 0}$, जेणेकरून आपण सहजपणे गणना करू शकता ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... अशा प्रकारे, आपल्या समीकरणाची एक किंवा दोन मुळे आहेत.

5. 5 गणना करा:${ displaystyle C = 3 {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } बरोबर) div 2}}}$. ${ प्रदर्शन शैली C}$ - सापडलेली ही शेवटची महत्त्वाची मात्रा आहे; हे आपल्याला समीकरणाच्या मुळांची गणना करण्यास मदत करेल. निर्दिष्ट सूत्रात मूल्ये बदला ${ displaystyle Delta _ {1}}$ आणि ${ displaystyle Delta _ {0}}$.
   • आमच्या समीकरणात:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 समीकरणाची तीन मुळे शोधा. सूत्रासह करा ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, कुठे ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, परंतु n च्या समान आहे 1, 2 किंवा 3... या सूत्रात योग्य मूल्ये बदला - परिणामी, तुम्हाला समीकरणाची तीन मुळे मिळतील.
   • येथे सूत्र वापरून मूल्याची गणना करा n = 1, 2 किंवा 3आणि नंतर उत्तर तपासा. जर तुम्ही तुमचे उत्तर तपासता तेव्हा तुम्हाला 0 मिळाले तर हे मूल्य समीकरणाचे मूळ आहे.
   • आमच्या उदाहरणात, पर्याय 1 मध्ये ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ आणि मिळवा 0, म्हणजे 1 समीकरणाच्या मुळांपैकी एक आहे.