सामग्री

• पावले
• 2 पैकी 1 पद्धत: टेबल
• 2 पैकी 2 पद्धत: बिनेट फॉर्म्युला आणि गोल्डन रेशो

फिबोनाची अनुक्रम ही संख्यांची मालिका आहे ज्यात प्रत्येक त्यानंतरची संख्या मागील दोन संख्यांच्या बेरजेइतकी असते. निसर्ग आणि कलेमध्ये सर्पिल आणि "सुवर्ण गुणोत्तर" च्या रूपात संख्या क्रमवारी आढळतात. फिबोनाची अनुक्रमांची गणना करण्याचा सर्वात सोपा मार्ग म्हणजे एक टेबल तयार करणे, परंतु ही पद्धत मोठ्या अनुक्रमांना लागू नाही. उदाहरणार्थ, जर तुम्हाला अनुक्रमातील १०० वी संज्ञा निश्चित करायची असेल तर बिनेटचे सूत्र वापरणे चांगले.

पावले

2 पैकी 1 पद्धत: टेबल

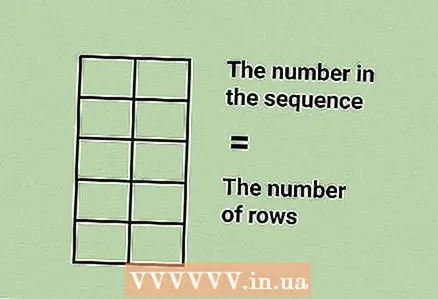1. 1 दोन स्तंभांसह एक टेबल काढा. सारणीतील पंक्तींची संख्या फिबोनाची अनुक्रमांकांच्या संख्येवर अवलंबून आहे.
   • उदाहरणार्थ, जर तुम्हाला क्रमाने पाचवा क्रमांक शोधायचा असेल तर पाच ओळींसह एक सारणी काढा.
   • सारणीचा वापर करून, मागील सर्व संख्यांची गणना केल्याशिवाय तुम्हाला काही यादृच्छिक संख्या सापडत नाही. उदाहरणार्थ, जर तुम्हाला अनुक्रमाची 100 वी संख्या शोधण्याची आवश्यकता असेल, तर तुम्हाला सर्व संख्यांची गणना करणे आवश्यक आहे: पहिल्यापासून 99 व्या पर्यंत. म्हणून, तक्ता केवळ अनुक्रमांचे प्रथम क्रमांक शोधण्यासाठी लागू आहे.
2. 2 डाव्या स्तंभात, अनुक्रमातील सदस्यांची क्रम संख्या लिहा. म्हणजेच, एकापासून सुरू होणाऱ्या क्रमाने संख्या लिहा.
   • अशा संख्या फिबोनॅकी अनुक्रमाच्या सदस्यांची (संख्या) क्रमांकाची संख्या निर्धारित करतात.
   • उदाहरणार्थ, जर तुम्हाला अनुक्रमाचा पाचवा क्रमांक शोधायचा असेल तर डाव्या स्तंभात खालील संख्या लिहा: 1, 2, 3, 4, 5. .
3. 3 उजव्या स्तंभाच्या पहिल्या ओळीवर 1 लिहा. फिबोनाची क्रमाचा हा पहिला क्रमांक (सदस्य) आहे.
   • हे लक्षात ठेवा की फिबोनाची अनुक्रम नेहमी 1. ने सुरू होतो. जर अनुक्रम वेगळ्या संख्येने सुरू होतो, तर तुम्ही पहिल्या पर्यंतच्या सर्व संख्यांची चुकीची गणना केली आहे.
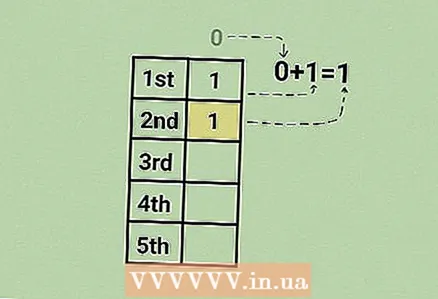4. 4 पहिल्या टर्म (1) मध्ये 0 जोडा. अनुक्रमातील हा दुसरा क्रमांक आहे.
   • लक्षात ठेवा: फिबोनाची अनुक्रमातील कोणतीही संख्या शोधण्यासाठी, फक्त मागील दोन संख्या जोडा.
   • अनुक्रम तयार करण्यासाठी, 1 (प्रथम टर्म) च्या आधी येणाऱ्या 0 बद्दल विसरू नका, म्हणून 1 + 0 = 1.
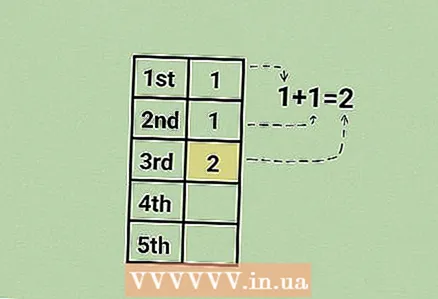5. 5 पहिल्या (1) आणि दुसऱ्या (1) अटी जोडा. अनुक्रमातील हा तिसरा क्रमांक आहे.
   • 1 + 1 = 2. तिसरी पद 2 आहे.
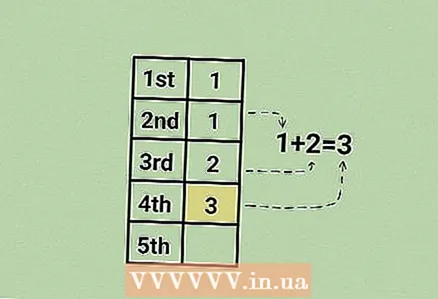6. 6 अनुक्रमातील चौथा क्रमांक मिळवण्यासाठी दुसरी (1) आणि तिसरी (2) संज्ञा जोडा.
   • 1 + 2 = 3. चौथी टर्म 3 आहे.
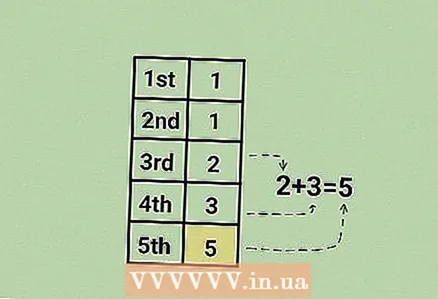7. 7 तिसरे (2) आणि चौथे (3) पद जोडा. ही क्रमवारीतील पाचवी संख्या आहे.
   • 2 + 3 = 5. पाचवी टर्म 5 आहे.
8. 8 फिबोनाची अनुक्रमातील कोणतीही संख्या शोधण्यासाठी मागील दोन संख्या जोडा. ही पद्धत सूत्रावर आधारित आहे: ${ displaystyle F_ {n} = F_ {n-1} + F_ {n-2}}$... हे सूत्र बंद नाही, म्हणून, या सूत्राचा वापर करून तुम्हाला मागील सर्व संख्यांची गणना केल्याशिवाय अनुक्रमाचा कोणताही सदस्य सापडत नाही.

2 पैकी 2 पद्धत: बिनेट फॉर्म्युला आणि गोल्डन रेशो

1. 1 सूत्र लिहा:${ displaystyle x_ {n}}$=${ displaystyle { frac { phi ^ {n} - (1- phi) ^ {n}} { sqrt {5}}}}$... या सूत्रात ${ displaystyle x_ {n}}$ - अनुक्रमाचे आवश्यक सदस्य, ${ प्रदर्शन शैली n}$ - सदस्याचा अनुक्रमांक, ${ displaystyle phi}$ - सोनेरी गुणोत्तर.
   • हे एक बंद सूत्र आहे, म्हणून मागील सर्व संख्यांची गणना न करता अनुक्रमातील कोणताही सदस्य शोधण्यासाठी त्याचा वापर केला जाऊ शकतो.
   • फिबोनाची संख्यांसाठी बिनेटच्या सूत्रावरून काढलेले हे एक सरलीकृत सूत्र आहे.
   • सूत्रात सुवर्ण गुणोत्तर आहे (${ displaystyle phi}$), कारण फिबोनाची अनुक्रमातील कोणत्याही सलग दोन संख्यांचे गुणोत्तर सुवर्ण गुणोत्तर सारखेच आहे.
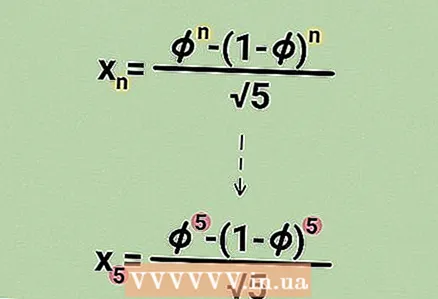2. 2 सूत्रामधील संख्येचा क्रम क्रमांक (त्याऐवजी n{ प्रदर्शन शैली n}).${ प्रदर्शन शैली n}$ अनुक्रमातील कोणत्याही इच्छित सदस्याची क्रमिक संख्या आहे.
   • उदाहरणार्थ, जर तुम्हाला अनुक्रमातील पाचवा क्रमांक शोधायचा असेल, तर सूत्रामध्ये 5 ला पर्याय द्या.सूत्र असे लिहिले जाईल: ${ displaystyle x_ {5}}$=${ displaystyle { frac { phi ^ {5} - (1- phi) {5}} { sqrt {5}}}}$.
3. 3 सुवर्ण गुणोत्तर सूत्रामध्ये बदला. सुवर्ण गुणोत्तर अंदाजे 1.618034 इतके आहे; हा नंबर सूत्रात जोडा.
   • उदाहरणार्थ, जर तुम्हाला अनुक्रमाचा पाचवा क्रमांक शोधायचा असेल, तर सूत्र असे लिहिले जाईल:${ displaystyle x_ {5}}$=${ displaystyle { frac {(1.618034) ^ {5} - (1-1.618034) ^ {5}} { sqrt {5}}}}$.
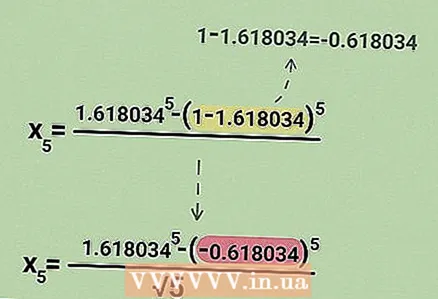4. 4 कंसातील अभिव्यक्तीचे मूल्यांकन करा. गणिती क्रियांच्या योग्य क्रम बद्दल विसरू नका, ज्यात प्रथम कंसातील अभिव्यक्तीचे मूल्यांकन केले जाते:${ displaystyle 1-1.618034 = -0.618034}$.
   • आमच्या उदाहरणात, सूत्र असे लिहिले जाईल: ${ displaystyle x_ {5}}$=${ displaystyle { frac {(1.618034) ^ {5} - ( - 0.618034) ^ {5}} { sqrt {5}}}}$.
5. 5 शक्तींना संख्या वाढवा. अंकामधील दोन संख्या योग्य शक्तींना वाढवा.
   • आमच्या उदाहरणात: ${ displaystyle 1.618034 ^ {5} = 11.090170}$; ${ displaystyle -0.618034 {5} = - 0.090169}$... सूत्र असे लिहिले जाईल: ${ displaystyle x_ {5} = { frac {11.090170 - ( - 0.090169)} { sqrt {5}}}}$.
6. 6 दोन संख्या वजा करा. भाग पाडण्यापूर्वी अंकामधील संख्या वजा करा.
   • आमच्या उदाहरणात: ${ displaystyle 11.090170 - ( - 0.090169) = 11.180339}$... सूत्र असे लिहिले जाईल: ${ displaystyle x_ {5}}$=${ displaystyle { frac {11,180339} { sqrt {5}}}}$.
7. 7 परिणाम 5 च्या वर्गमूळाने विभाजित करा. 5 चे वर्गमूल अंदाजे 2.236067 आहे.
   • आमच्या उदाहरणात: ${ displaystyle { frac {11.180339} {2.236067}} = 5.000002}$.
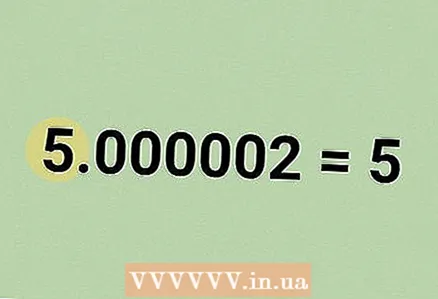8. 8 निकालाला जवळच्या पूर्ण संख्येवर गोल करा. शेवटचा परिणाम दशांश अपूर्णांक असेल जो पूर्णांक जवळ आहे. अशा पूर्णांक म्हणजे फिबोनाची अनुक्रमांची संख्या.
   • जर तुम्ही तुमच्या गणनेत गोलाकार नसलेल्या संख्या वापरल्या तर तुम्हाला पूर्णांक मिळेल. गोलाकार संख्यांसह कार्य करणे खूप सोपे आहे, परंतु या प्रकरणात आपल्याला दशांश अपूर्णांक मिळेल.
   • आमच्या उदाहरणात, तुम्हाला दशांश 5.000002 मिळाले. पाचवा फिबोनाची क्रमांक मिळवण्यासाठी जवळच्या पूर्ण संख्येवर गोल करा, जो 5 आहे.